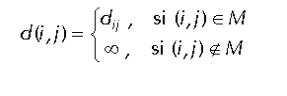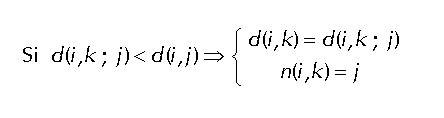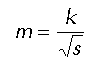|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Departamento de Ingeniería en Sistemas de Información | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Propiedades
de un algoritmo de Enrutamiento. Clasificación
de los métodos de Enrutamiento. En
función de las tablas de Enrutamiento empleadas. Enrutamiento
fijado en origen. Comparación
entre ambos tipos de Enrutamiento. Algoritmos
de camino más corto. Algoritmo
de Floyd - Warshall. Algoritmo
de Bellman - Ford distribuído. Algoritmos
de aprendizaje. (Backward Learning) Árbol
de expansión de bridges. Comparación Source Routing - Transparent Bridges. Establecimiento
de vecindades. Presentación del probelma. Protocolos
de Enrutamiento existentes. Características
del retardo y caudal. Soluciones.
Mecanismos de control de congestión. Algoritmos
de control de congestión. Algoritmo
de paquetes reguladores. Algoritmo
de descarte de paquetes. Enrutamiento y Control de Congestión Introducción.Trataremos de dar unas nociones básicas de lo que se entiende por Enrutamiento, estableciendo los objetivos que persigue un algoritmo de este tipo en una red de conmutación de paquetes, y acabaremos enumerando las propiedades que debe tener un algoritmo de Enrutamiento. Objetivos del EnrutamientoPodemos definir Enrutamiento como un proceso mediante el cual tratamos de encontrar un camino entre dos puntos de la red: el nodo origen y el nodo destino. En esta definición tenemos que matizar el hecho de que cuando hablamos de un camino nos estamos refiriendo a varios, el mejor o el mejor para llegar de 1 a N puntos. Habría que tener en cuenta también la capilaridad de las redes (conexión de los nodos con los terminales de usuario, por lo que no se trataría de buscar un camino entre dos nodos, sino entre dos terminales. En realidad, resolviendo lo primero tenemos resuelto lo segundo, por lo que nosotros enunciaremos nuestro problema como la búsqueda de un camino de conexión entre dos nodos de la red. El objetivo que se persigue es encontrar las mejores rutas entre pares de nodos j-k . Para ello tendremos que establecer lo que se entiende por mejor ruta y la métrica que se emplea para determinarla.:
Nos centraremos en redes de conmutación de paquetes, tanto en modo datagrama como en modo circuito virtual.
El problema no es trivial, como puede parecer a simple vista, para redes reales, puesto que hay que tener en cuenta los cambios de carga de los enlaces y los cambios de configuración (debidos a altas y bajas, a averías en los nodos, etc.). Llegados a este punto conviene matizar que el Enrutamiento busca el camino óptimo, pero como el tráfico varía con el tiempo, el camino óptimo también dependerá del instante en que se observa la red. Los protocolos serán los encargados de ocultar la red y comprobar que las condiciones impuestas se verifican siempre. Por esta razón, el Enrutamiento debe proveer a la red de mecanismos para que ésta sepa reaccionar ante situaciones como: Variabilidad del tráfico: se han de evitar las congestiones de la red. Variaciones topológicas, como las mencionadas arriba: caídas de enlaces, caídas de nodos, altas y bajas ... Cambios en la QoS (Quality of Service): a veces se pide un servicio donde no importa el retardo y sí un alto throughput, y viceversa. Se tiene un sistema distribuído, donde cada nodo debe tener un cierta inteligencia y se produce un procesamiento independiente de cada nodo (no hay proceso central). También es un sistema asíncrono, en el sentido de que no hay un momento determinado para que ocurran las cosas (un nodo transmite cuando le llega información, y esto sucede a su vez cuando el usuario decide mandarla). Propiedades de un algoritmo de Enrutamiento.Para que un algoritmo de Enrutamiento real funcione de forma razonable debe cumplir las siguientes propiedades: Corrección. Es algo obvio: queremos que el paquete llegue precisamente al nodo al que lo mandamos. Simplicidad. Debe aportar soluciones sencillas. Esto es útil para redes reales (grandes) y los protocolos mas simples son los que en la actualidad tienden a imponerse (p.e. RIP: Routing Interconexion Protocol). Robustez. Debe comportarse correctamente frente a posibles problemas (caída de enlaces...), que deben haber sido previstos de antemano. Estabilidad. Es muy importante que se cumpla. El procedimiento debe converger antes de que la red cambie de estado (caída de nodo, alta de usuario, etc.). Cuando esto ocurre, se recalculan de nuevo las rutas, debiendo los nodos llevar a cabo acciones coherentes que conduzcan a situaciones estables. Equidad o Justicia. Debe tratar a todos los usuarios de la misma manera. Gestionabilidad (trazabilidad). Supone tener información (trazas) de lo que ha hecho la red para que en el caso de que ocurran "cosas raras" sea posible corregirlas. Escalabilidad. Tengo que tener un comportamiento optimo sea cual sea el numero de nodos ( incluso si este aumenta mucho) Métodos de Enrutamiento.Introducción.En este apartado veremos primero la estructura de un nodo de conmutación de paquetes, lo cual nos valdrá para hacer una posterior clasificacíon de los métodos de Enrutamiento atendiendo a la forma en la que los nodos recogen y distribuyen la información que les llega de la red y a otros factores. Estructura de un nodo.Podemos tomar como representación de un nodo la siguiente figura: Figura 5 Esquema de un nodo
Pasamos a describir cada uno de sus elementos: FIB
(Forward Information Base) Es la tabla de Enrutamiento que se consulta para hacer el reenvío de los paquetes generados por los usuarios (los PDU representan estos paquetes). Entorno local Contiene la información de lo que el nodo ve (memoria disponible, enlaces locales, etc.), más la que hay que proporcionarle. PDU
(Protocol Data Unit) Unidad fundamental de intercambio de información para un nivel determinado (a veces se indica explícitamente el nivel poniendo N-PDU, o PDU de nivel N), como nivel de enlace, red, etc. Son llamados también tramas. R-PDU
(Routing-PDU) Paquete de control. Estos paquetes los mandan otros nodos con información sobre la red (no son datos). Por ejemplo, se manda información de que el nodo sigue activo, y también las distancias a otros nodos (vector de distancias). Decisión Contiene la lógica necesaria para decidir si la tabla de Enrutamiento debe ser cambiada. RIB
(Routing Information Base) Es la base de información de Enrutamiento que se consulta para decidir y formar la FIB. La información de la RIB se consigue mediante interacción con el entorno local de cada nodo (cada nodo observa sus enlaces) y mediante la recepción de R-PDUs d e información de control procedentes de otros nodos vecinos que informan del conocimiento que estos nodos tienen sobre el estado de la red. A su vez, con la información obtenida por la RIB, ésta manda PDUs de control para informar del conocimiento del estado de la red que el nodo tiene a los demás nodos. Clasificación de los métodos de Enrutamiento.Los métodos de Enrutamiento los podemos clasificar en función de: El procedimiento de Enrutamiento. Las tablas de Enrutamiento empleadas.
En función del procedimiento.Los procedimientos de Enrutamiento pueden ser: EstáticoLas tablas de Enrutamiento de los nodos se configuran de forma manual y permanecen inalterables hasta que no se vuelve a actuar sobre ellas. La adaptación a cambios es nula. Tanto la recogida como la distribución de información se realiza por gestión (se realiza de manera externa a la red), sin ocupar capacidad de red. El calculo de ruta se realiza off-line (en una maquina especifica),y las rutas pueden ser las optimas al no estar sometido al requisito de tiempo real. Este tipo de Enrutamiento es el optimo para topologias en los que solo hay una posibilidad de Enrutamiento (topologia en estrella). CuasiestáticoEste Enrutamiento, es igual que el estatico pero en vez de dar una sola ruta fija, se dan además varias alternativas en caso de que la principal no funcione, de ahí que tenga una adaptabilidad reducida. Este tipo de Enrutamiento puede dar lugar a situaciones incoherentes, ya que no se enteran todos los nodos de los problemas de la red, sino sólo los adyacentes a los problemas. CentralizadoEn este tipo de Enrutamiento, todos los nodos son iguales salvo el nodo central, que recoge la información de control de todos los nodos y calcula la FIB (tabla de Enrutamiento) para cada nodo, es decir, el nodo central decide la tabla de Enrutamiento de cada nodo en función de la información de control que éstos le mandan. El inconveniente de este metodo es que consumimos recursos de la red, y se harian necesaria rutas alternativas para comunicarse con el nodo central. La adaptación a cambios es perfecta siempre y cuando las notificaciones de los cambios lleguen antes de iniciar los cálculos de las rutas. AisladoSe basa en que cada vez que un nodo recibe un paquete que tiene que reenviar (porque no es para él) lo reenvía por todos los enlaces salvo por el que le llegó.
DistribuídoEn este tipo de Enrutamiento todos los nodos son iguales, todos envían y reciben información de control y todos calculan, a partir de su RIB (base de información de Enrutamiento) sus tablas de Enrutamiento. La adaptación a cambios es optima siempre y cuando estos sean notificados. Hay dos familias de procedimientos distribuídos: Vector de distanciasCada nodo informa a sus nodos vecinos de todas las distancias conocidas por él, mediante vectores de distancias (de longitud variable según los nodos conocidos). El vector de distancias es un vector de longitud variable que contiene un par (nodo:distancia al nodo) por cada nodo conocido por el nodo que lo envia, por ejemplo (A:0;B:1;D:1) que dice que el nodo que lo manda dista "0" de A,"1" de B y "1" de D, y de los demás no sabe nada (ésta es la forma en la que un nodo dice lo que sabe en cada momento). El nodo solo conoce la distancia a los distintos nodos de la red pero no conoce la topologia. Con todos los vectores recibidos, cada nodo monta su tabla de Enrutamiento ya que al final conoce qué nodo vecino tiene la menor distancia al destino del paquete, pues se lo han dicho con el vector de distancias. Estado de enlacesCada nodo difunde a todos los demás nodos de la red sus distancias con sus enlaces vecinos, es decir, cada nodo comunica su entorno local a todos los nodos. Así cada nodo es capaz de conocer la topología de la red. La clave y dificultad de este metodo es la difusión. A continuación se muestra una tabla comparativa de todos los tipos de Enrutamiento vistos Clasificación de los métodos de Enrutamiento
En los Enrutamientos estático y cuasi-estático
la información necesaria se recoge y envía mediante gestión (al
crear la red y en operaciones de mantenimiento), y los cálculos de la FIB se
realizan off - line (mediante gestión, es decir en una máquina a
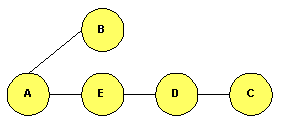
parte). Comparación VD - EE.Haremos una comparación entre los algortitmos de vector de distancias y de estado de enlaces, ambos del tipo distribuído: Consumo de capacidad.Lo ideal es que el tráfico de control sea lo más pequeño posible. Con vectores de distancia se transmiten vectores cuyo tamaño es del orden del número de nodos de la red pues cada nodo comunica a su vecino todas las distancias que conoce; con procedimientos de estado de enlace, el tamaño del tráfico enviado es siempre el mismo independientemente del tamaño de la red. En consecuencia, consume más capacidad un vector de distancias. Consumo de memoriaEl Enrutamiento basado en estado de enlace hace que cada nodo almacene toda la topología de la red, sin embargo con vectores de distancias sólo ha de almacenar distancias con el resto de los nodos. Luego consume más memoria en los nodos un procedimiento basado en estado de enlace. Adaptabilidad a los cambiosEl método de vector de distancia es más sencillo, pero se adapta peor a los cambios que el de estado de enlace. Esto es porque mientras que este último tiene información de toda la red, el primero sólo sabe a quién tiene que reenviar un paquete, pero no tiene información de la topología. Luego se adapta mejor un Enrutamiento de estado de enlaces. No obstante, el Enrutamiento basado en vector de distancias es mucho menos complejo que el de estado de enlaces, cosa que en algunos casos prácticos puede llegar a ser muy importante. En función de las tablas de Enrutamiento empleadas.Los nodos manejan tablas de Enrutamiento, en las que aparece la ruta que deben seguir los paquetes con destino a un nodo determinado de la red. Podemos distinguir entre Enrutamiento salto a salto y Enrutamiento fijado en origen. Nosotros veremos con detalle sólo el primer tipo (salto a salto). Enrutamiento salto a saltoEn la literatura inglesa, este tipo de encaminamineto se denomina como hop by hop. Se basa en que cada nodo no tiene que conocer la ruta completa hasta el destino, sino que sólo debe saber cuál es el siguiente nodo al que tiene que mandar el paquete: las tablas dan el nodo siguiente en función del destino. Como ejemplo, tomemos la siguiente red:
Las tablas de Enrutamiento de los nodos A y B serán: Tabla 1 Tablas de Enrutamiento para la red de la Figura 5
En la tabla de Enrutamiento de cada nodo debera aparecer
una entrada en el campo destino por cada nodo que se pueda alcanzar desde el
citado nodo, y en el campo siguiente nodo aparecerá el nodo vecino al
que se debera enviar los datos para alcanzar el citado nodo destino. Las
soluciones propuestas no son únicas, pudiendo elegir otros caminos que
minimicen el tiempo de retardo, el número de saltos, etc. La única condición
que se impone es que debe haber consistencia: si, por ejemplo, para ir de A
aB pasamos por C, entonces para ir de B a C no
podremos pasar por A, porque entonces se formaría un bucle y el
paquete mandado estaría continuamente viajando entre los nodos B y A,
como puede comprobarse fácilmente. Enrutamiento fijado en origen.En inglés este Enrutamiento se llama source routing. En él, son los sistemas finales los que fijan la ruta que ha de seguir cada paquete. Para ello, cada paquete lleva un campo que especifica su ruta(campo RI:Routing Information), y los nodos sólo se dedican a reenviar los paquetes por esas rutas ya especificadas. Así pues, son los sistemas finales los que tienen las tablas de Enrutamiento y no se hace necesaria la consulta o existencia de tablas de Enrutamiento en los nodos intermedios. Este tipo de Enrutamiento suele ser típico de las redes de IBM. Tabla 2 Tablas de Enrutamiento para la red de la Figura 5
Comparación entre ambos tipos de Enrutamiento.Lo veremos por medio de la siguiente tabla: Tabla 3 Comparación entre Enrutamiento salto a salto y fijado en origen
Los bucles (situación que se da cuando los paquetes pasan más de una vez por un nodo) ocurren porque los criterios de los nodos no son coherentes, generalmente debido a que los criterios de Enrutamiento o no han convergido después de un cambio en la ruta de un paquete; cuando por cualquier causa un paquete sufre un cambio de Enrutamiento, la red tarda en adaptarse a ese cambio pues la noticia del cambio tiene que llegar a todos los nodos. Es en ese transitorio cuando se pueden dar los bucles, ya que unos nodos se han adaptado y otros no. El objetivo de los algoritmos de Enrutamiento es detener el curso de los paquetes antes de que se produzcan bucles. Esto es importante sobre todo cuando se envían los paquete s por varias rutas simultáneamente (técnicas de inundación, etc..., que veremos más adelante).
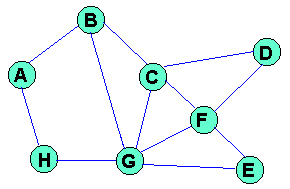
Algoritmos de Enrutamiento.Introducción.En este apartado tras tratar brevemente la teoria de grafos, veremos distintos algoritmos de Enrutamiento. En concreto, veremos algoritmos de camino más corto, en los que cada nodo decide cuál es el camino más corto hacia un destino, en función de la información de control que recibe de otros nodos de la red, algoritmos aislados, en los que los nodos no intercambian información de control explícitamente, y algoritmos de difusión, que permiten hacer llegar un paquete a todos los nodos de una red. Notación. Teoría de grafos.Necesitamos revisar el concepto de distancia o coste de un canal. Es una medida de la calidad de un enlace en base a la métrica que se haya definido (por ej., para el método de Gerla es la sensibilidad al aumento de tráfico; otras veces es coste económico, probabilidad de error, etc.). En la práctica se usan varias métricas simultáneamente. Para el desarrollo de los siguientes conceptos vamos a tomar como ejemplo la siguiente red (donde los números situados sobre cada enlace indican el coste del mismo):
y sobre ella vamos a definir: Árbol de expansión (Spanning tree) de una red. Es un subconjunto del grafo que representa toda la red y tiene las siguientes caracteristicas: Mantener la conectividad: es posible alcanzar cualquier nodo desde cualquier otro. Eliminar los lazos: no hay bucles topológicos. Contiene a todos los nodos de la red. Este tipo de grafo no es único; un ejemplo sobre la red anterior es:
Se suele usar cuando se desea hacer una inundación, ya que si todos los nodos tienen en su tabla de Enrutamiento el mismo árbol de expansión, no se producirán bucles y todos los paquetes llegan a todos los nodos. Se usa sobre todo en difusiones. Arbol de expansión de coste o distancia mínima (Minimun Spaning Tree) Es un árbol de expansión que cumple que el sumatorio de distancias que emplea es mínimo. Por ejemplo el anterior tiene coste 10. El siguiente es mínimo (su suma de distancias es 5; esto se puede comprobar sumando el peso de las distancias de cada canal, tal y como aparecen en la Figura 1); no existe otro con suma de distancias menor, aunque en general podría haberlo, es decir, el árbol de expansión de coste mínimo no es único, aunque en la práctica se escoge uno y se trabaja con él en lo sucesivo.
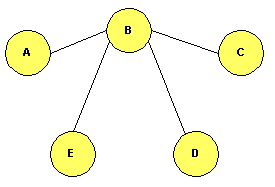
Arbol divergente (Sink tree) de un nodo. Es un árbol con origen en un nodo y ramas a todos los restantes nodos. No produce bucles. Hay un árbol divergente por cada nodo; sin embargo, normalmente se trabaja con un sólo árbol de expansión para toda la red (lo cual no quiere decir que no haya muchos árboles de expansión diferentes, aunque se trabaje con uno sólo acordado por toda la red). Determina las distancias más cortas de ese nodo al resto de los nodos: el sumatorio del peso de los enlaces es mínimo entre el nodo raíz y cualquier otro. Es, expresada de forma gráfica, la tabla de Enrutamiento de cada nodo.
No se debe confundir el arbol divergente (Sink Tree) con el arbol de expansión de peso mínimo (MST), aunque pueden coincidir. En el primero minimizamos las distancias del nodo raíz a cada uno de los demás nodos, mientras que en el segundo lo que minimizamos la suma de las distancias de los enlaces. Algoritmos de camino más corto.Estos algoritmos minimizan el coste o distancia de la ruta que une dos nodos cualesquiera. Por ejemplo, si la métrica utilizada es el número medio de saltos, el algoritmo de camino más corto será el que minimice este número de saltos entre los nodos que pretendemos conectar.
Algoritmo de Dijkstra.Halla el camino de mínima distancia entre un nodo origen (o raiz) y cualquier otro nodo de la red. Puede verse que esto equivale a decir que construye el árbol divergente de la red. La idea es construir el camino de distancia más corta en orden de longitud de camino creciente, es decir, se va iterando con la distancia, seleccionando en cada caso el nodo más cercano. A cada nodo se le asigna una etiqueta, que es un indicador de la distancia del nodo origen al nodo en cuestión. Así, se hace una partición de la red: se crea un conjunto de nodos con etiqueta permanente (conjunto P) y un conjunto de nodos con etiqueta tentativa (conjunto T), es decir, un conjunto de nodos cuya etiqueta puede cambiar en las siguientes iteraciones. El algoritmo en detalle es el siguiente: Paso 0: Iniciación.
es decir, el único nodo con etiqueta permanente es el origen (con etiqueta "cero"). Para los demás, la etiqueta es la distancia al nodo origen (dij). Paso 1: Encontrar el nodo más cercano.
Si P contiene todos los nodos, PARAR (algoritmo completo).
Paso 2: Actualización de etiquetas.
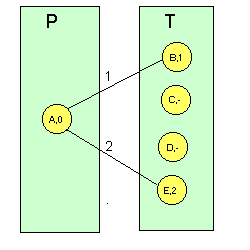
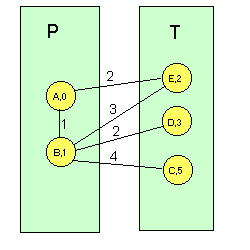
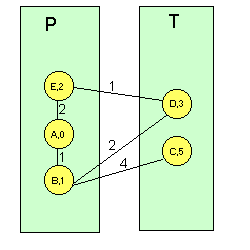
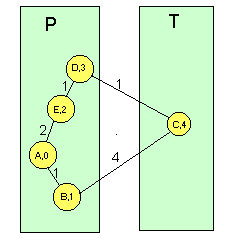
Ir al paso 1. Si hay que elegir entre dos etiquetas iguales, se elige cualquiera de ellas (no se soporta balanceo de carga). Para comprender mejor este algoritmo, veamos un ejemplo sobre la red de la Figura 1 tomando como nodo origen el A. En las siguientes figuras, el número que va sobre cada enlace representa la distancia física entre nodos y el número que hay en cada nodo representa su etiqueta (un guión representa una etiqueta de valor infinito: no hay conexión directa entre cualquier nodo con etiqueta permanente y el nodo con dicha etiqueta): Figura 6 Ejemplo de algoritmo de Dijkstra sobre la red de
la Figura 1
Por último, meteríamos el nodo C en la partición
de nodos con etiqueta permanente, siendo su etiqueta "4" (se accedería
a través del nodo D). Como puede comprobarse, este algoritmo tiene una complejidad de N2 operaciones. Para calcular las mejores distancias entre todo par de nodos, la complejidad es del orden de N3 operaciones. No obtiene directamente las tablas de Enrutamiento, sino las distancias
entre nodos. Para obtener las tablas de Enrutamiento hay que fijarse en los
caminos que va escogiendo en cada iteración, que le sirven para actualizar
las etiquetas. Algoritmo de Floyd - Warshall.A diferencia del algoritmo anterior (algoritmo de Dijkstra), que consideraba un nodo origen cada vez, este algoritmo obtiene la ruta más corta entre todo par de nodos (todos con todos). Itera sobre el conjunto de nodos que se permiten como nodos intermedios en los caminos. Empieza con caminos de un solo salto y en cada paso ve si es mejor la ruta de la iteración anterior o si por el contrario conviene ir por otro nodo intermedio más(aquél sobre el cual se itera). Para ello se construye la matriz D, cuyos elementos, Dij, son las etiquetas (indicadores de distancia) de la ruta entre el nodo i y el j. El algoritmo es el siguiente: Paso 0: Iniciación.
donde dij es la distancia entre el nodo i y el nodo j.
Paso 1: Iteración.
En cada paso se ve si es mejor la ruta de la iteración anterior o si es mejor ir a través del nodo n. Para la red de la Figura 1 se tiene la siguiente secuencia de matrices: Nota: El nodo 1 es el nodo A de la red, el 2 es el B y así sucesivamente.
Podemos comprobar que la primera fila de la matriz (distancias del nodo A a todos los demás) coincide con las etiquetas halladas con Dijkstra en el apartado anterior. La última matriz es la matriz de distancias buscada, ya que se han probado todos los nodos intermedios. Hay que tener en cuenta que el algoritmo da sólo la menor distancia; se debe manejar información adicional para encontrar tablas de Enrutamiento. La complejidad de este algoritmo es del orden de N3, igual que para Dijkstra. Para un Enrutamiento distribuído con estado de enlaces es mejor Dijkstra, que tiene una menor complejidad para un nodo dado. Algoritmo de Bellman - Ford.Encuentra la mínima distancia de un nodo dado al resto de los nodos, y si se lleva información adicional, proporciona las tablas de Enrutamiento, al igual que los anteriores. Itera sobre el número de saltos, h, es decir, se busca el mejor camino, el de distancia más corta, con la restricción de llegar al destino en un número de saltos h (número de la iteración). No encuentra las mejores rutas hasta que el algoritmo no se ha ejecutado por completo. Sea el nodo 1 aquél para el que queremos encontrar las mejores rutas al resto de nodos. El algoritmo es el siguiente:
Iniciación
lo que equivale a decir que con cero saltos todos los nodos distan del nodo 1 una distancia infinita, salvo él mismo que dista cero.
Iteración
Se prueba dando un salto más. Notar que está permitido el caso i=j, resultando entonces que no se da un nuevo salto (era mejor la ruta hallada antes). Tiene una complejidad del orden de N3 por cada nodo que realiza el algoritmo, es decir, un orden mayor que Dijkstra. El interés del algoritmo radica en que se asemeja al de una red en la que se parte de la ignorancia total de un nodo, en la siguiente iteración conoce a sus nodos vecinos y así va progresivamente conociendo nodos más lejanos. Puede verse que esta es la forma de trabajar de un Enrutamiento mediante vector de distancias. Para ello, necesita ser enunciado de forma distribuída, de la forma que vemos a continuación. Algoritmo de Bellman - Ford distribuído.Es la base de un algoritmo de vector de distancias: permite obtener en cada nodo la minamiento n(i,j). Se ejecuta en cada nodo i. El algoritmo es el siguiente:
Iniciación.
donde M es el conjunto de nodos vecinos al nodo i.
Al principio sólo se sabe llegar al conjunto de nodos vecinos. Actualización.
y realiza la siguiente actualización de su tabla de Enrutamiento:
Una vez actualizada la tabla, propaga la distancia d(i,k) a vecinos. El proceso de actualización se sigue repitiendo: cuando un nodo i recibe un vector de distancias de un nodo vecino j, calcula las distancias a todos los demás nodos k a través del vecino j, y si es mejor que por el camino anterior se actualiza la tabla de Enrutamiento del nodo i, ( n(i,k)=j) y las nuevas distancias d(i,k). Una vez obtenido el nuevo vector de distancias, i se lo manda a los demás nodos j para que éstos actualicen a su vez los suyos. Vemos un ejemplo para el nodo A de la red de la Figura 1. Inicialmente, este nodo tiene conocimiento de las distancias a sus vecinos B yE) por lo que su vector de distancias sería (A,0; B,1; E,2). Cuando le llega el vector de distancias de B, que sería (A,1; B,0; C,4; D,2; E,3), el nodo A realiza los cálculos descritos y se da cuenta de que puede llegar a E, D y C a través de B, siendo el vector de distancias resultante (A,0; B,1; C,5; D,3; E,2). Así, A pone en su tabla de Enrutamiento que C y D son accesibles a través de B y manda el vector calculado sus nodos vecinos, que a su vez calculan un nuevo vector de distancias. Esto se repite hasta que todos los nodos saben dónde deben mandar un paquete para que llegue a su destino a través de un camino de distancia mínima. Este algoritmo presenta inconvenientes:
Los vectores de distancia son proporcionales al tamaño de la red. Entonces no se tiene un buen comportamiento para redes grandes. Los nodos no conocen la topología de la red, por lo que pueden aparecer bucles transitorios hasta que la situación converja hacia un conocimiento suficiente por parte de los nodos. Algoritmos aislados.En este apartado se pretende dar diferentes opciones para encaminar en una red mediante mecanismos aislados (los nodos no se intercambian información ). Podemos distinguir dos clases de algoritmos para un Enrutamiento de este tipo, que son algoritmos de aprendizaje y algoritmos de inundación. Ejemplos concretos de este tipo de algoritmos hay muchos, como el llamado algoritmo de Hot Potato. Algoritmos de inundación.En este algoritmo los nodos no intercambian información de control. Cuando un paquete llega a un nodo de la red, lo que éste hace es conmutarlo por todos los puertos de salida sin mirar ninguna tabla de Enrutamiento. De esta forma se asegura que el paquete llegue al destino. Problema: si la topología presenta bucles el paquete estará dando vueltas de manera indefinida. Como consecuencia, se consume capacidad de red ilimitada. Solución: La solución pasa por limitar la vida del paquete en la
red, es decir, establecer una caducidad. Cuando se genera un
paquete se incluye en un campo el número máximo de saltos que éste puede
dar. Cada vez que ese paquete es conmutado el campo "número de
saltos" se decrementa en una unidad hasta que sea cero, en cuyo caso los
nodos ya no lo conmutan, sino que lo descartan. De esta manera
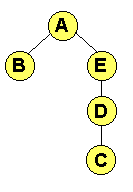
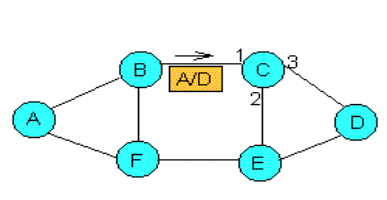
aseguramos una existencia limitada de paquete dentro de la red. Otra solución es determinar si un nodo ha conmutado ya ese paquete. En este caso, un nodo origen marca el paquete generado con un número de secuencia de tal forma que la unicidad de ese paquete viene dada por el par (origen, secuencia). Cuando un nodo conmuta un paquete mira en tabla; si ya lo ha conmutado lo descarta, y si no lo ha conmutado lo introduce en la tabla. Como ventaja respecto de la solución anterior se consume menos capacidad de red, pero posee el inconveniente de que la tecnología del nodo es muy compleja y el tamaño de las tablas puede ser muy grande. Además esta solución puede dar mayores retardos que la anterior. Concluyendo, la inundación es buena si tenemos la red sobredimensionada, ya que no tendríamos tantas limitaciones en cuanto a ocupación de recursos. En este caso, la inundación es el algoritmo más robusto y óptimo, ya que encuentra todas las rutas, entre ellas la mejor. Por último, queda solucionar el problema de multiplicidad de paquetes en el nodo destino, pero eso queda para los niveles superiores de la jerarquía OSI. Algoritmos de aprendizaje. (Backward Learning)Son los usados en redes locales. Cuando llega un paquete a un nodo con destino a otro nodo cualquiera, se hace lo siguiente: Si no se conoce el nodo destino se inunda y se incrementa el campo número de saltos dados por el paquete.(al contrario que en inundación, donde se decrementaba). Si el destino se conoce, se envia el paquete por la ruta que se indica en las tablas. El aprendizaje se basa en que partimos de no tener ninguna información de control, y segun se van produciendo inundaciones se aprende. Cuando llega un paquete se mira el origen , el puerto a través del que ha llegado y el número de saltos dados por ese paquete hasta que ha llegado. Si no teníamos ninguna entrada en la tabla de Enrutamiento con el nodo del que ha llegado o si la teniamos pero con numero de saltos mayor (mayor distancia) se actualizan las tablas. Para evitar que un paquete esté dando vueltas eternamente en la red y por lo tanto consuma recursos innecesariamente, se limita el número de saltos que éste puede dar. En principio, cuando todos los nodos hayan aprendido las mejores rutas se acabará la inundación. Sin embargo, a las entradas se les asocia un tiempo de vida, que se renueva cada vez que se hace uso de la entrada. Si transcurrido el tiempo de vida la entrada no ha sido empleada se borra, volviendo a inundar. Así se logra que la red se adapte a los cambios. Veamos esto con un ejemplo. Sea la red de la figura siguiente: Figura 7: Red ejemplo para algoritmo aislado.
Al nodo C le llega por la puerta 1 un paquete con origen en A y destino D. Puede ser que C no sepa dónde está situado el nodo D pero aprende que A es accesible por la puerta 1, y escribe esta información en su tabla de Enrutamiento. Así, si le llega luego un paquete con destino al nodo A, lo mandará por la puerta 1. Problema: la inundación consume recursos indefinidamente y pueden aparecer bucles. Esto puede evitarse añadiendo un poco de control: en los paquetes se introduce información sobre el número de saltos que ha realizado éste (se tiene un contador que se incrementa en cada salto); cuando este número llega a un valor máximo, se descarta el paquete. De esta forma podemos cuantificar distancias además de conocer la conectividad entre dos nodos. Este tipo de algoritmos es óptimo (consiguen la mejor ruta, ya que en realidad consiguen todas), siempre que se controle que no se saturen los enlaces de los nodos. Estos algoritmos se llaman de Backward Learning, o aprendizaje hacia atrás, debido a que la forma que tienen de aprender los nodos es a través de la información que les llega del nodo origen.
Algoritmos de difusión.Queremos conseguir que un paquete que sale de un nodo llegue a todos los demás. Este procedimiento encuentra una aplicación directa para un Enrutamiento basado en estado de enlaces, puesto que la información sobre los estados de los enlaces se difunde a toda la red En general, lo que se hará será mandar paquetes a todos los nodos y marcarlos para deshabilitarlos si vuelven a pasar (para evitar bucles). Veremos cuatro métodos de conseguir la difusión:
1er método: consiste en enviar paquetes a todos los demás nodos (tráfico unicast). Este método es poco eficiente porque por un mismo nodo pasan varios paquetes iguales, además de que no elimina el problema de la formación de bucles. Por ejemplo, en la red de la Figura 7, para encaminar de A a D hay que difundir de A a todos los demás nodos, incluyendo D; entonces, entramos en un bucle. 2o método: hace una inundación: se manda un paquete de un nodo origen a todos los demás. Este tampoco es un buen método, porque consume muchos recursos y también puede hacer que aparezcan bucles. 3er método: se usa el árbol de expansión. Deshabilitamos algunos enlaces de forma que todos los nodos estén conectados pero sin bucles. Así, al inundar se consigue tener muy pocos envíos. Es una solución bastante usada, aunque la forma de acordar entre todos los nodos de la red qué enlaces se deshabilitan es complicada. 4o método: se hace un reenvío por ruta hacia atrás (Reverse Path Forwarding). No requiere calcular el árbol de expansión. Los nodos tienen calculadas las rutas, y cuando tienen que ayudar a difundir no siempre se hace inundación: se mira la dirección origen del paquete; si llega por el enlace que utiliza el nodo para ir al origen inunda; si llega por otra ruta el nodo considera que el paquete esta dando vueltas y lo descarta. Por ejemplo, en la red de la Figura 7 el nodo C tiene en su tabla de Enrutamiento que los paquetes con origen en A le llegan por la puerta 1; entonces, si le llega un paquete con origen en A por esa puerta inunda y en caso contrario lo descarta.
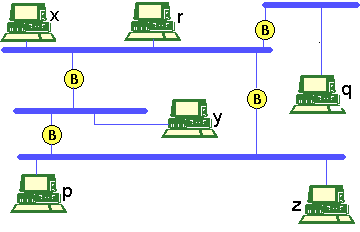
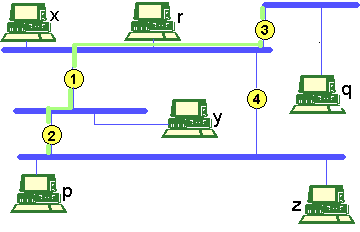
Aplicaciones.Introducción.En este apartado haremos un resumen de los métodos de Enrutamiento vistos hasta ahora en base a proponer soluciones para el Enrutamiento en una red como la de la figura siguiente: Figura 8 Caso práctico de red
La figura representa una interconexión de redes locales
de ordenadores. Queremos resolver el problema del envío de un paquete de un
ordenador a otro cualquiera. Las redes locales están interconectadas mediante
bridges (marcados con una B). Bridges.Se denomina bridge a un elemento de rutado (nodo) que almacena y envía tramas entre LANs (Local Area Network). Pueden verse como "repetidores" de nivel 2. Es, por tanto, un dispositivo de interconexión de redes que opera a nivel de enlace. Suele ser una máquina dedicada, cuya arquitectura de comunicaciones está dividida en dos partes, cada una con la estructura de la red local a la que está conectado. Las razones por la que se usan brigdes para interconectar redes y no se hace de manera directa (p.e. uniendo coaxiales) son las siguientes: Interconexión de subredes diferentes: las tramas pueden ser distintas, en cuyo caso los sistemas finales no se entenderían. Interconexion de LANs distantes Separacion de tráfico: si un segmento está saturado no carga con tráfico dirigido a ese mismo segmento a los demás tramos de la red, disminuyendo así la probabilidad de colisiones en el resto de los segmentos. Lo que se pretende es que la mayor parte del tráfico de un segmento se quede en él. Aumento de fiabilidad: debido a que los bridges sirven para adoptar rutas alternativas. Seguridad: se puede configurar el bridge para que no se deje entrar a un segmento a todo aquel que quiera acceder. En general, con un bridge se pueden resolver algunos aspectos problemáticos de la interconexión de redes. Pero hay otros que no son capaces de solucionarlos. Veamos a continuación la problematica a resolver entre LANs: Diferentes formatos de trama: el bridge debe encontrar equivalencias entre ambas. (Por ejemplo, Ethernet-Token Ring). Diferentes velocidades de transmisión: en este caso el Bridge debe almacenar las tramas que recibe y retransmitirlas al otro segmento a la velocidad de éste. Diferentes tamaños de las tramas: el bridge no es capaz de solucionar esto. Un ejemplo de esta situacion es la interconexión de redes Ethernet con Token Ring: la primera requiere tramas menores de 1.5 Kbytes, mientras que la segunda puede enviar tramas de mayor tamaño. El bridge es una solución heterodoxa al problema de interconexión de redes. Hay situaciones que no sabe resolver (como el caso anterior). En cambio, lo que sí resuelve es el Enrutamiento. Vamos a ver los dos modos de funcionamiento de los bridges, el modo transparente y el modo source routing.
Bridges transparentes.Se dice que un bridge es transparente cuando no es tenido en cuenta por los sistemas finales, esto es, ellos envían las tramas a los otros sistemas como si pertenecieran a la misma red local. No requieren ningún tipo de configuración (PLUG AND PLAY). Podemos distinguir tres tipos de bridges transparentes: básico, Learning Bridge y Spanning tree Bridge. Bridge básico.Este tipo se basa en un algoritmo de inundación. Es muy sencillo, pero genera muchos problemas. El bridge escucha en modo promiscuo todas las tramas de cada LAN a la que está conectado y las difunde a las restantes por los puertos de salida. Supongamos que el nodo x de la Figura 8 quiere mandar un paquete al nodo r. Todos los bridges inundarán a las otras redes conectadas a ellos. Sin embargo, x y r pertenecen a la misma red local, por lo que no sería necesario. Descubrimos así varios inconvenientes: Se generan copias de paquetes de una línea de entrada a todas las de salida: el algoritmo es muy ineficiente ya que se están mandando tramas a sitios donde no está el destino. Hay una explosión de tráfico, debido a lo dicho anteriormente, por lo que se consume más capacidad de red. Se generan bucles de tráfico. Este tipo no aporta nada respecto a la solución de poner un repetidor (a menos que se trate de redes distintas) Learning Bridge.En la Figura 8 cada uno de los nodos marcados con una B es un bridge. En concreto, estaremos interesados en los llamados Learning Bridges, o bridges de aprendizaje, caracterizados por: escuchar en modo "promiscuo" en todas sus interfaces (o puertos). por cada trama recibida, almacenan en una tabla (cache) la dirección origen y el puerto por el que llegó. Los nodos oyen por dónde llegan los mensajes de un determinado equipo y mandan los paquetes a ese equipo por ahí. Cuando les llega una trama, consultan si su dirección destino está en la tabla: SÍ: se envía a través del interfaz que indica la tabla (si es el mismo por el que llegó se descarta). NO: se envía por todos los interfaces, salvo por el que llegó (inundación). Aparece un problema debido a que los equipos pueden moverse de una red local a otra, en cuyo caso, si habíamos aprendido la dirección de un equipo todos los paquetes destinados a él irán sólo por el camino antiguo, con lo que se perderán. Esto se soluciona añadiendo una entrada más a la tabla llamada aging time, o tiempo de actualización, transcurrido el cual, si no se han recibido paquetes de una dirección determinada, se borra la entrada correspondiente, con lo que el siguiente paquete que llegue con destino al nodo cuya entrada se ha borrado será reenviado mediante inundación. Esta solución obedece a dos fines: Evitar un crecimiento excesivo de las tablas (el número de terminales puede ser muy alto). Detectar cambios en la configuración de los segmentos. Como se quiere que los Bridges trabajen en modo transparente, es necesario que se den cuenta de estos cambios. Esta solución es mejor que la del Bridge básico , pero no soluciona el problema de los bucles. Puede comprobarse que en la red de la Figura 7 si, por ejemplo, el equipo que no ha transmitido ningún paquete y el equipo x quiere comunicarse con él, el paquete que le envía éste estará dando vueltas por la red si no se pone alguna solución a ello, como por ejemplo llevar la cuenta de las veces que pasa el paquete por un nodo, y descartarlo cuando llegue a un número máximo prefijado. Pero esto no es posible debido a que al trabajar en modo transparente no se pueden modificar las tramas para incluir en ellas un campo que contenga el número máximo de saltos. Árbol de expansión de bridges.En la terminología inglesa, esto se llama Spanning Tree Bridges. Es una solución que solventa el problema de bucles. Todos los bridges se ponen de acuerdo en usar una topología sin bucles (Spanning Tree, o árbol de expansión sobre la cual funcionan como bridges transparentes). En concreto, estaremos interesados en construir el árbol de coste mínimo. Las características de este tipo son: Topología arbitraria. Plug and play. Bridges transparentes. Seguimos el siguiente algoritmo: Se elige la raíz. Se calcula la distancia mínima desde cada bridge a la raíz. En cada LAN se selecciona un bridge determinado (el más próximo a la raíz), que se utilizará para enviar tramas desde la LAN a la raíz. En cada bridge se elige un puerto para enviar tramas a la raíz. Una vez elegido el Spanning Tree, cada bridge utiliza sus puertos incluídos en él para enviar tramas. El resto quedan inactivos. En definitiva, se trata de crear una topología libre de lazos. Tomando como origen la red de la Figura 8, podemos construir el siguiente Spanning Tree:
Figura 9 Ejemplo de Spanning Tree sobre la red de la Figura 8
donde se ha supuesto que el nodo raíz es el nodo 1.
El spanning tree se ha marcado en color más claro, y se ha supuesto
que es mejor llegar a la red de la que cuelgan p y z a través
del nodo 2 que a través del nodo 4. Vemos que de esta forma el
nodo 4 queda totalmente inoperativo (éste es el inconveniente de este
algoritmo, ya que hay redes para las que se desaprovechan bastantes recurso). Para construir el árbol de expansión o mantenerse en contacto para poder solucionar posibles cambios de configuración (caída de enlaces...) los Bridges intercambian tramas CBPDU (Configuration Bridge Protocol Data Unit). En esta trama hay varios campos: Destino, donde se pone una dirección multicast (que indica que va dirigida a todos los Bridges de ese segmento. Estas tramas multicast no se propagan, sino que son consumidas por los Bridges. Root Id.: indica qué Bridge es la raiz del árbol de expansión. Transmitting Bridge Id.: identifica al Bridge que transmite la trama. Cada Bridge posee un identificador único. Coste: es la distancia del Bridge que envía la trama al Bridge raiz. Los campos principales que maneja el algoritmo visto en este apartado son los tres últimos. Al principio cada bridge se toma a sí mismo como raiz.. A medida que van intercambiando CBPDU van seleccionando el Bridge raiz y configurando el árbol de expansión en base a la mejor trama. Para elegir la mejor trama toma el siguiente algoritmo: Es mejor CBPDU si el RootId es menor. Si el coste es menor. Si el TransmittingId. es menor Si el puerto es menor. Source
Routing Bridges.
En este modo de funcionemiento son los sistemas finales quienes fijan la ruta que deben seguir las tramas. Para conocer las rutas se usan unas tramas de control que recorren todas las posibles rutas al destino y almacenan en un campo especial el camino seguido. El destino constesta cada trama que le llega por el camino indicado en el campo. Cuando las contestaciones llegan al origen, éste decide la mejor ruta (generalmente la que menos retardo tenga). Veamos los pasos que se siguen en la búsqueda de una ruta desde un sistema final X a otro Y: Se envía una trama del tipo "All paths explorer" (o Discovery) con dirección destino Y. A medida que atraviesa la red, la trama se irá replicando y cada copia guardará el camino seguido. Además el campo "Máx. trama" se va actualizando. Y devuelve a X todas las tramas recibidas, convirtiéndolas previamente a tramas con una ruta específica e invirtiendo el bit de sentido. X elige una ruta en función de las tramas recibidas de Y. Comparación
Source Routing - Transparent Bridges.
Existe un problema de incompatibilidad a la hora de que coexistan Bridges transparentes y Source Routing en la misma subred. La solución que adoptó IEEE fue que todos los Bridges soportaran el modo transparente. Así tenemos dos configuraciones posibles: Bridges
Transparentes SRTB
(Source Routing Transparent Bridges): Bridges Transparentes con capacidad de
Source Routing. El Bridge transparente ha calado más en el mercado, aunque en entornos IBM se usa Source Routing . Para más información existen unas transparencias dadas en clase. Protocolos de Enrutamiento.Introducción.Una gran red no se puede resolver como una sola red, ya que esto conduciría a tablas de Enrutamiento gigantescas o intercambio de información entre miles y miles de nodos. Por ello a la hora de tratar un gran red se procede a dividirla en partes mas pequeñas o dominios ,dentro del cual se usa un único protocolo de Enrutamiento (elegido por el operador de la red),y luego se interconectan todas las partes o dominios. Se define como dominio de Enrutamiento o sistema autónomo a la sección p parte de la red que posee un único administrador de recursos. Podemos distinguir dos tipos de Enrutamientos: Intradominio: Para el Enrutamiento dentro de cada dominio, buscando en todo momento el encontrar los caminos óptimos. Interdominio: Es el que se encarga de alcanzar la "conectividad total", no busca caminos óptimos si no garantizar la alcanzabilidad. Como ejemplo citaremos que en tecnología IP (Internet), el intradominio es IGP (Internal Gateway Protocol), y el Interdominio es EGP (External Gateway Protocol).dentro de los que existen recomendaciones distintas. Protocolos intradomino.
Establecimiento de vecindades. Presentación del probelma.Dentro de una subred nos encontramos que los terminales o sistemas finales de una subred tienen conectividad física entre si, y además existirá un router que garantizara la conexión con el exterior. Cada terminal posee unas direcciones físicas (únicas y planas de 48 bits), y además unas direcciones lógicas o de intered (dirección IP). Las direcciones IP son 32 bits en los que existen dos partes: Prefijo (de longitud variable y igual para todos los elementos de la subred) y Numero de sistema. El problema viene cuando nosotros queremos comunicar dos sistemas finales de los que conocemos sus direcciones IP pero no existe ningún sistema intermedio que maneje estas direcciones. Para solucionar este problemas existen varias soluciones: Asociación directa: Construcción de forma estática de unas tabla estáticas que a cada dirección lógica le asignen una dirección física. Que las direcciones lógicas contengan a las direcciones físicas. Asociación dinámica: Se emplean protocolos de resolución de direcciones, que de forma automática establecen las tablas .
Solución TCP/IP.A solución adoptada en internet ( TCP/IP), se basa en el empleo de los protocolos ARP (Address Resolution Protocol) e ICMP. Este protocolo consiste en lo siguiente: Cuando X desea enviar algo a Y ( X conoce la dirección lógica de Y pero necesita la dirección física) , X procede a preguntar a Y su dirección física. Par lograrlo se envía un paquete ARP encapsulado en una trama 802.3 , dicho paquete ARP dispone de tres campos : Origen, Destino y Mensaje ARP. El sistema final X rellena los el campo origen con su dirección física y lógica y pone en el destino unicamente la dirección lógica. Este mensaje será exclusivamente contestado por Y que rellenará el campo dirección física del destino y enviara el paquete de vuelta a X encapsulado en una trama 802.3 unicast. De cara a evitar tener que mandar excesivo numero de tramas ARP cuando un sistema envía en difusión su dirección física al preguntar por la de otro, todo los demás sistemas se la aprenden. Además para evitar tablas grandes se emplean técnicas d caché. Para posibilitar la existencia de estaciones sin disco se hace necesario que estas puedan llegar a conocer su dirección lógica de alguna manera, para ello se ha implementado el protocolo RARP (Reverse Address Resolution Protocol). Cuando una maquina de estas características arranca lo que hace es difundir una petición para conocer su dirección lógica , incluyendo en la misma su dirección física. Esta petición llegara a una maquina encargada de proporcionar las direcciones lógicas (RARP Server) que contesta. Protocolos de Enrutamiento existentes.
RIP
(Routing Information Protocol): Es un algoritmo de vector de distancias, que emplea como métrica el numero de saltos ( se encuentra limitado entre 1 y 16= infinito). Existen dos tipos de usuarios los activos y los pasivos ( no transmiten sol o reciben)Los nodos activos cada 30sg. Difunden un vector de distancias que solo procesan los routers o sistemas intermedios. Los pasivos escuchan los mensajes enviados por los activos y actualizan (recalculan) sus tablas. Para garantizar que los nodos aprendan de noticias perores cada 2 min (120s) se produce el borrado de las tablas. En este tipo de protocolo existen dos tipos de paquetes: Request: enviados por los routers o hosts que acaban de conectarse o su información a caducado. Response: enviados periodicamente en respuesta a un paquete request o cuando cambia algún coste. Este protocolo tiene la ventaja de que es muy sencillo y por tanto muy empleado. Sin embargo no existe interoperabilidad entre las distintas implementaciones existentes, tiene una convergencia lenta (inconsistencias transitorias) ,puede crear bucles y además la métrica no tiene en cuenta la velocidad de los enlaces, las cargas, etc. El tamaño de la red esta limitado por el numero de saltos máximo (limitado a 15) y además este protocolo no soporta subnetting (mascaras). HELLO: Usa el vector de distancias como el RIP sin embargo en este protocolo la métrica empleada es el retardo. Para calcular el retardo, cuando un nodo transmite a un nodo vecino pone la fecha y la hora local, y cuando el paquete llega al nodo vecino este mira su reloj y calcula la diferencia, con este dato actualiza las rutas . Para conseguir esto es necesario garantizar la sincronización de los relojes, aspecto bastante complejo de conseguir. Este proceso tiene la ventaja de que tiene en cuenta la carga y la velocidad de los enlaces, pero es muy probable que se produzcan oscilaciones para ello solo se cambia la ruta si la mejora es sensible, es decir se coloca un umbral (p.e. 150% mas rápido). De esta forma se evita que por diferencias de ms se cambie la ruta optima. OSPF
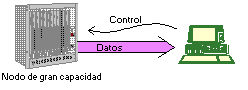
(Open Shortest Path First): Es el mejor aunque todavia esta en fase de desarrollo. Las carcteristicas mas diferenciadoras son que usa el estado de enlaces, soporta subnetting y es capaz de emplear varias métricas. Este protocolo es capaz por si solo es capaz de suministrar mecanismos para jerarquizar la red y descubrir dinamicamente los sistemas intermedios. Hay routers de area y de sistema autónomo. Los primeros solo hablan con los de esa area, es decir sus tablas de Enrutamiento tienen como entradas los nodos de su area y una adicional para salir al exterior. Los segundos (routers de sistema autónomo) calculan rutas entre areas, por ello tienen como entradas tantas como areas hay en su nivel de jerarquia mas una para subir un nivel en la jerarquia. Control de congestión.Introducción.En este apartado trataremos el tema de la congestión de las redes. Comenzaremos haciendo una distinción entre control de flujo y control de congestión: Control de flujo. Es una técnica que permite sincronizar el envío de información entre dos entidades que producen/procesan la misma a distintas velocidades. Por ejemplo, supongamos el caso representado en la siguiente figura:
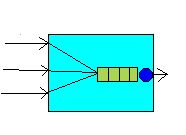
Figura 10 Conexión entre nodo de alta capacidad y PC
En este caso, dada la gran velocidad a la que produce y
envía información, el nodo desborda al PC, por lo que éste debe enviar
información de control (control de flujo) para que el nodo reduzca su tasa de
envío de datos. De esta forma , parando a la fuente cada cierto tiempo, el PC
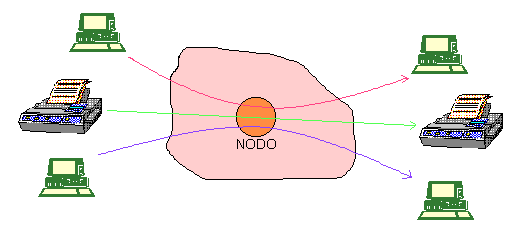
puede procesar el tráfico que le envía el nodo. Control de congestión. Es un concepto más amplio que el control de flujo. Comprende todo un conjunto de técnicas para detectar y corregir los problemas que surgen cuando no todo el tráfico ofrecido a una red puede ser cursado, con los requerimientos de retardo, u otros, necesarios desde el punto de vista de la calidad del servicio. Por tanto, es un concepto global, que involucra a toda la red, y no sólo a un remitente y un destinatario de información, como es el caso del control de flujo. Figura 11 Congestión en un nodo
El control de flujo es una más de las técnicas para
combatir la congestión. Se consigue con ella parar a aquellas fuentes que
vierten a la red un tráfico excesivo. Sin embargo, como veremos, hay otros
mecanismos. Una vez hecha esta distinción, en los sucesivos apartados veremos
características del retardo y del caudal, veremos distintas causas de aparición
de congestión, analizaremos las soluciones que se proponen para este problema
y acabaremos viendo distintos algoritmos de control de congestión. Características del retardo y caudal.El caudal depende del tipo de red y tiene un valor nominal máximo, que no podremos superar en ningún caso. Pero además, la red no ofrece el mismo caudal real si se le ofrece poco tráfico o si se le ofrece mucho. Veamos la siguiente figura:
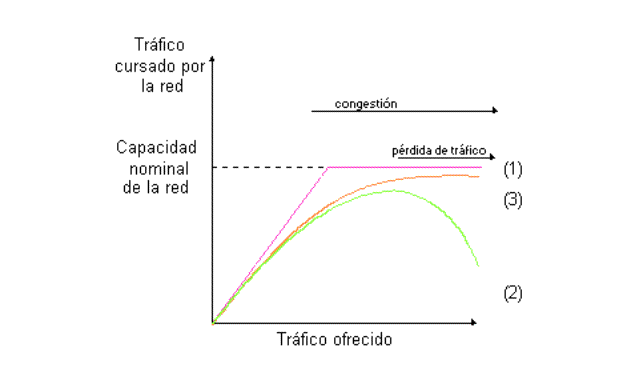
Figura 12 Caudal en función del tráfico ofrecido
La curva (1) representa el comportamiento ideal de la red: hay linealidad hasta llegar a la capacidad nominal de la red, momento en el que el tráfico cursado se satura. La curva (2) representa el comportamiento real típìco de una red. Como puede observarse, al llegar a la zona de saturación, cuanto más tráfico se ofrece menos tráfico se cursa. Esto es debido, por ejemplo, a que los paquetes tardarán mucho tiempo en llega r a su destino, y mientras tanto serán retransmitidos por la fuente, pensando que se han perdido por el camino. Esto, a su vez, origina una explosión de tráfico, ya que cada paquete es retransmitido varias veces, hasta que consigue llegar a tiempo al destino.
El retardo de tránsito en la red sigue la siguiente curva:
Figura 13 Retardo de tránsito en función del tráfico ofrecido
Vemos que el retardo no aumenta linealmente, sino que el
aumento de éste es mayor que el aumento de tráfico ofrecido. Causas de la congestión.Hay varias causas de congestión. Enumeraremos aquí las más importantes: Memoria insuficiente de los conmutadores. Por ejemplo, veamos la siguiente figura: Figura 14 Saturación del buffer de un nodo
En ella se tiene un conmutador en el que tres líneas de entrada mandan paquetes a una de salida. Así puede llenarse el buffer (cola) de la línea de salida.
Insuficiente CPU en los nodos. Puede que el nodo sea incapaz de procesar toda la información que le llega, con lo que hará que se saturen las colas.
Velocidad insuficiente de las líneas. Se tiene el mismo problema que en el caso anterior. Soluciones. Mecanismos de control de congestión.El problema del control de congestión puede enfocarse matemáticamente desde el punto de vista de la teoría de control de procesos, y según esto pueden proponerse soluciones en bucle abierto y en bucle cerrado. Soluciones en bucle abierto. También llamadas soluciones pasivas. Combaten la congestión de las redes mediante un adecuado diseño de las mismas. Existen múltiples variables con l as que el diseñador puede jugar a la hora de diseñar la red. Estas variables influirán en el comportamiento de la red frente a la congestión. Las resumiremos en función del nivel del modelo OSI al que hacen referencia:
Soluciones en bucle cerrado. También llamadas soluciones activas. Actúan cuando se detectan problemas. Tienen tres fases: Monitorización de parámetros. Reacción: envío de información a los puntos necesarios. Ajuste del sistema. El mecanismo que permite la reacción del sistema frente a estos problemas puede ser: Realimentación explícita. Los nodos próximos a saturarse envían información hacia atrás comunicando esta situación. Realimentación implícita. La permiten los mecanismos de asentimiento de la red. Por ejemplo, IP realiza realimentación implícita midiendo el tiempo que tarda en llegar el paquete de asentimiento a una transmisión. Algoritmos de control de congestión.Veremos un algoritmo en bucle abierto llamado mecanismo de Traffic Shaping y dos algoritmos en bucle cerrado llamados algoritmo de paquetes regulador es y algoritmo de descarte de paquetes. Mecanismo de Traffic Shaping.Significa conformado de tráfico. Es un mecanismo en bucle abierto. Conforma el tráfico que una fuente puede inyectar a la red. Se usa en redes ATM (Asynchronous Transfer Mode; tecnología de red orientada a conexión; en estas redes, la velocidad de línea es de 155 Mbps y el usuario puede ver una velocidad de unos 10 Mbps. Si se tiene una ráfaga lista para transmitir, el sistema obliga a no transmitir todo seguido (conforma el tráfico). Requiere un acuerdo entre proveedor y cliente: el proveedor garantiza que se cursa el tráfico si se transmite a una tasa determinada y tira el tráfico si se supera. Esto lo realiza mediante una función policía, que es un nodo que tira los paquetes que superan la tasa contratada a la entrada de la red (no se tiran una vez que ya ha entrado). Esto puede realizarse mediante un algoritmo de Leaky Bucket, cuyo nombre se debe a que es como si tuviéramos un bidón que vamos llenando con un caudal determinado y por el que sale el líquido (Leaky: hace aguas) con otro caudal distinto; si llenamos muy deprisa el bidón acabará llenándose y vertiéndose por arriba, lo que asemeja una pérdida de paquetes en una red. Veamos un ejemplo con un sistema codificador de imágenes:
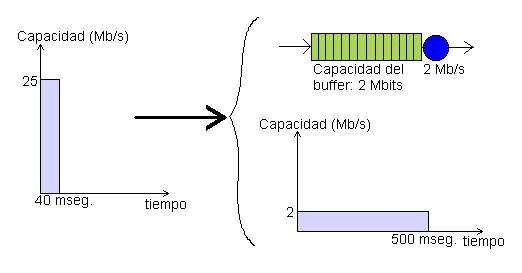
Figura 15 Ejemplo de mecanismo de Leaky Bucket
Este sistema codifica la señal de video y la envía a ráfagas.
Para ser transmitida necesita ser conformada: se almacenan muestras en
un buffer y después se transmiten a velocidad constante. Si se
sobrepasa el caudal predeterminado, pueden tirarse paquetes en el regulador
(por parte del usuario) o en la función policía (por parte del
proveedor). Este sistema permite aplanar ráfagas, como puede verse en la
siguiente figura, donde la situación de la izquierda representa un sistema
con tráfico no conformado y la de la derecha la equivalente si se conforma y
se contrata transmisión a 2Mbps (la fuente transmite ráfagas de 1 Mb a 25
Mbps): Figura 16 Ejemplo de aplanamiento de ráfagas con tráfico conformado
Algoritmo de paquetes reguladores.En terminología inglesa, al paquete regulador se le llama choke packet. Se hace en bucle cerrado. Asocia un peso u a cada línea que cambia con el tiempo según la ecuación:< P
donde:
un: función de peso, que depende del instante actual a través de f y del anterior a través de un-1. f: tiene un valor "0" si no transmitimos en el instante actual o "1" si transmitimos. a: constante comprendida entre 0 y 1 y que da más importancia al instante actual o al instante anterior según su valor. Si n supera un cierto umbral, se pone la línea en estado de alerta y se considera que puede haber congestión. Si llegan paquetes a esa línea, se envía un aviso hacia atrás con un paquete regulador que indica esta situación. Además, en los paquetes que se envían hacia delante se pone un flag a "1" para indicar al resto de los nodos que no manden paquetes reguladores hacia atrás, ya que el nodo origen está avisado. Al llegar el paquete regulador al origen, se reduce el flujo (por ejemplo, a la mitad). Si pasa un determinado tiempo sin recibir notificaciones de congestión, se vuelve a subir el flujo que puede cursar el origen. Si por el contrario se supera un umbral mayor, se pasa directamente a hacer descarte de paquetes. Variaciones: Pueden mandarse paquetes reguladores con información de estado (grave, muy grave, etc.) En vez de monitorizar las líneas de salida pueden medirse otros parámetros, tales como el tamaño de las colas en los nodos. Con el mecanismo descrito se tarda mucho en reaccionar. Entonces, puede hacerse regulación salto a salto, en la que se dice al nodo anterior que mande la información por otro sitio si es posible. Algoritmo de descarte de paquetes.Es un algoritmo de control de congestión en bucle cerrado. Se basa en que los nodos descartan (tiran) paquetes cuando su ocupación es alta. Para esto los nodos han de conocer sus recursos (CPU y memoria). Hace una asignación dinámica de los buffers en base a las necesidades de cada línea. Sin embargo, cada línea necesita al menos una (o más) posiciones de memoria para gestionar información relevante, tal como asentimientos, que permite la liberación de posiciones de memoria ocupadas por paquetes que estaban esperando por si necesitaban retransmitirse. Si a la línea llegan datos (no asentiminentos u otra información relevante) y el buffer de salida de la línea correspondiente está lleno, se descarta el paquete. Hay varias formas de hacer la asignación de buffers: En base al uso. No es muy eficiente, porque cuando una línea se empieza a cargar acapara todos los recursos. Asignación fija. Tampoco es muy buena, ya que desaprovecha recursos. Asignación subóptima (de Irland). Llamando k al número de posiciones del buffer y s al número de líneas de salida, se tiene que el número de posiciones de memoria asociadas a cada línea es:
Bibliografía
http://selva.dit.upm.es/~cd/apuntes Tanenbaum,
Andrew S., Computer
Networks, Prentice-Hall, 1996. Bertsekas,
D. y Gallager, R.,
Data Networks, 2a edición, Prentice-Hall, 1992. Comer,
Douglas E., Internetworking
with TCP/IP, 3a edición, Volumen 1: Principles,
Potocols and Architectures, Prentice-Hall, 1995.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||