Ejercicio 1: Identificar en el Ejercicio 2 de Derivaciones (punto anterior) la clasificación de Chomsky

que le corresponde a cada uno de los conjuntos de producciones dadas.

 Resolución:

1-       TIPO 3

2-       TIPO 2

3-       TIPO 2

4-       TIPO 2

5-       TIPO 2

6-       TIPO 2

7-       TIPO 2

  Ejercicio 2:  Dada la siguiente Gramática:

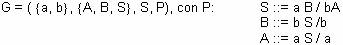
 Indique si las siguientes cadenas pueden ser generadas o no por esta gramática (demostrarlo

mediante la derivación), en caso afirmativo, determine su árbol de derivación. Para ello, considere

las siguientes cadenas:    

x = “abbaaab”,  y = “baabbaaaabb”,   z= “baabab”,  p = “abbaab”

 Resolución:

-          x no puede ser generada por la gramática.

-          y no puede ser generada por la gramática.

-          z si puede ser generada por la gramática.

-          p si puede ser generada por la gramática.

 1-       equivalentes

2-       ambiguas

3-       recursivas

indicando lo que sucede en cada una de las siguientes producciones (demostrarlo):

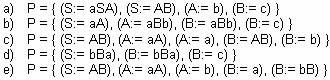
Resolución:

a)       Recursiva directa por izquierda (S:= aSA)

b)       Recursiva directa (B:= aBb)

c)       Recursiva directa por derecha (A:= aA, B:= AB) y ambigua

d)       Recursiva directa (B:= bBa)

e)       Recursiva directa por derecha (A:= aA) y ambigua

NINGUNA ES EQUIVALENTE

 Ejercicio 4: Determine la definición algebraica y los árboles de derivación correspondiente,

considerando las siguientes reglas gramaticales:

 Resolución:

 P1: “hay recursividad”

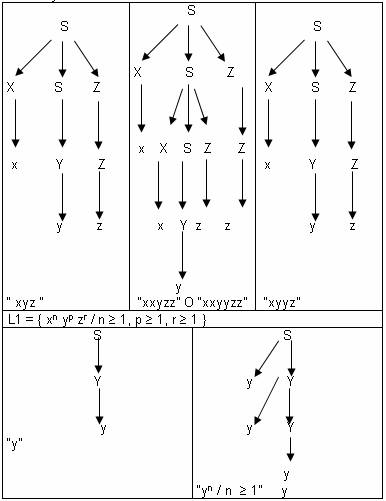
 P2: “hay recursividad”

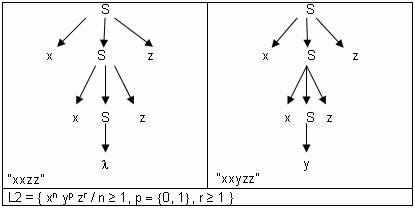
P3: “hay recursividad”

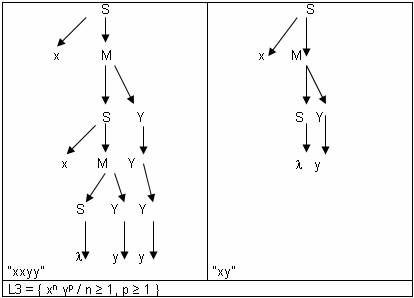
 Ejercicio 5: Considerando como 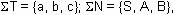 cuyo axioma es S = S,

establecer si las reglas de producción dadas a continuación, corresponden a gramáticas

equivalentes. Justifique su respuesta, (demostrarlo):

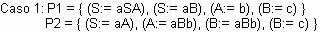
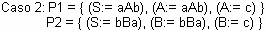
 Resolución:

 Caso 1: P1 y P2 no son equivalentes.

Caso 2: P1 y P2 no son equivalentes.