|
Introducción
Las gramáticas se utilizan para describir lenguajes.
Existe una primera clasificación para las
gramáticas, y esta estará en función a los tipos de
lenguajes que genere, esto es ya sean lenguajes
naturales o lenguajes formales.
Un lenguaje natural es como el Español o el Inglés o
como cualquier otro lenguaje de comunicación entre
personas, en donde la estructura de las frases, se
describen por medio de una gramática que agrupa las
palabras en categorías sintácticas tales como
sujetos, predicados, frases preposicionales,
etcétera. Estas construcciones gramaticales surgen
como un intento de explicar las formas admitidas por
el Lenguaje, con las cuales se construyen las
frases, aunque en su definición se presentarán
excepciones gramaticales.
Un Lenguaje Formal, por el contrario surge a partir
de su gramática, y por lo tanto no presenta
excepciones en su definición. Esto es así, porque
los Lenguajes Formales son los que se utilizan para
que se comuniquen los hombres con las máquinas. De
esta manera a partir de las gramáticas formales es
como surgen los Lenguajes de Programación.
Gramáticas para describir Lenguajes Naturales
Para poder describir a los Lenguajes Naturales,
podemos escribir reglas como las que enumeramos en
el siguiente conjunto
 : :

Vale la pena destacar que esta es “una versión muy
simplificada” de la gramática castellana, y si bien
da lugar a oraciones que son correctas en nuestro
idioma, también puede generar oraciones que resulten
incorrectas desde el punto de vista tanto semántico
(de su significado), como sintáctico (de su
estructura).
Este es el caso de:
El árbol juega (incorrecta
semánticamente)
Los madre come risueño (incorrecta
sintácticamente)
Estos errores se solucionan en la lengua castellana
agregando reglas que regulan y restringen las
combinaciones de terminales y que corresponden al
análisis morfológico y semántico del lenguaje. (En
los lenguajes formales no existe el análisis
morfológico que es el de género, número y persona,
es decir el que controla la concordancia entre
sujeto y verbo o la concordancia entre artículo,
sustantivo y adjetivo)
Gramáticas Formales
Estas gramáticas permitirán en forma intencional
describir en determinado lenguaje; esto se hará
definiendo el alfabeto sobre el que se construirán
sus palabras, denominadas símbolos terminales;
un símbolo inicial del que se partirá para la
obtención de cualquier de las palabras del lenguaje
llamado axioma inicial, un conjunto de
símbolos especiales denominados no terminales,
los que permitirán expresar representaciones o
estados intermedios en el proceso de generación de
las palabras del lenguajes; y un conjunto de reglas
de producciones o de reescritura, que serán las que
permitan realizar las transformaciones necesarias,
partiendo desde el axioma inicial, produciendo los
reemplazos de símbolos no terminales, mediante la
utilización de las reglas de producción hasta
obtener las palabras del lenguaje.
Definición
Un
gramática formal G, es una 4-tupla,
que queda definida de la siguiente manera:
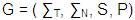
En donde:
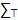 : Conjunto de Símbolos que representan el
Alfabeto de Símbolos Terminales, en donde toda
palabra del lenguaje generado por esta gramática,
estará formada por símbolos o caracteres definidos
en este conjunto.
: Conjunto de Símbolos que representan el
Alfabeto de Símbolos Terminales, en donde toda
palabra del lenguaje generado por esta gramática,
estará formada por símbolos o caracteres definidos
en este conjunto.
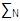 : Conjunto de Símbolos que representan el
Alfabeto de Símbolos No Terminales. Éste conjunto de
símbolos será utilizado como símbolos auxiliares en
la derivación de cadenas, pero no formaran parte de
las cadenas del lenguaje.
: Conjunto de Símbolos que representan el
Alfabeto de Símbolos No Terminales. Éste conjunto de
símbolos será utilizado como símbolos auxiliares en
la derivación de cadenas, pero no formaran parte de
las cadenas del lenguaje.
De las definiciones anteriores se observa lo
siguiente:
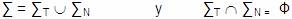
S: Símbolo No Terminal especial, que pertenece
al conjunto de Símbolos No Terminales ( S
Î
∑N ), denominado símbolo inicial o Axioma
de la Gramática.
P: Conjunto finito de reglas o producciones que
tienen como única restricción que en la parte
izquierda debe haber al menos un símbolo no
terminal.
Ejemplo:
dada la gramática
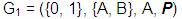
Donde
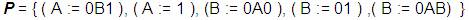
También podríamos escribirlas:
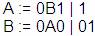
Producciones
Una producción, o regla de producción es un par
ordenado de palabras ( x, y ), con x e
y Î 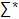 ,
donde la presencia de x se encuentra como
parte integrante de cualquier otra palabra, puede
ser sustituida por y; lo que permite
transformar palabras en otras. ,
donde la presencia de x se encuentra como
parte integrante de cualquier otra palabra, puede
ser sustituida por y; lo que permite
transformar palabras en otras.
Como notación suele utilizarse x := y,
denominada notación BNF ( por Backus - Naur Form,
por sus creadores ).
La palabra x es denominada la parte
izquierda o primer miembro de la
producción; y la palabra y, la parte
derecha o segundo miembro.
Simbología:
:=
Serán producciones el conjunto P de la
gramática de ejemplo
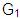 : :

Derivación directa
Es la aplicación directa de una producción ( x :=
y), a una determinada palabra v para convertirla en
w.
Simbología: 
Ejemplo:
dado v = z . x . u ; y aplicando ( x := y)
obtenemos w = z . y . u
Con v, w, z, u  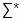 . .
Para el caso de la gramática G1, podemos partiendo
de una palabra 0B1, obtener, aplicando las reglas de
producción (B : = 0A0 ) lo siguiente: 0B1  00A01 00A01
Derivación
Es la aplicación de una secuencia de producciones a
una palabra
Simbología:  * *
Ejemplo:
En el ejercicio anterior continuaremos aplicando
reglas de producción y pasaremos de una palabra 0B1
a una palabra 0000101
0B1
 00A01 00A01
 000B101 000B101
 00001101 00001101
Derivación por la izquierda
Si al aplicar las reglas de producción se producen
los reemplazos de símbolos no terminales que se
encuentren mas a la izquierda de la cadena en la que
se debe producir el reemplazo.
Ejemplo:
En el ejercicio anterior continuaremos aplicando
reglas de producción y cuando se presente la
alternativa de que símbolo aplicar, lo haremos
eligiendo el que se encuentre mas a la izquierda.
El conjunto de producciones es:
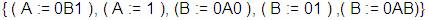
A
 0B1 0B1
 00AB1 00AB1
 000A0B1 000A0B1
 0000B10B1 0000B10B1
 00000110B1 00000110B1
 00000110011 00000110011
Derivación por la derecha
Si al aplicar las reglas de producción se producen
los reemplazos de símbolos no terminales que se
encuentren mas a la derecha de la cadena en la que
se debe producir el reemplazo.
Ejemplo:
En el ejercicio anterior continuaremos aplicando
reglas de producción y cuando se presente la
alternativa de que símbolo aplicar, lo haremos
eligiendo el que se encuentre mas a la derecha.
El conjunto de producciones es:
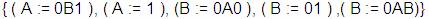
A
 0B1 0B1
 00AB1 00AB1
 00A0AB1 00A0AB1
 00A0A011 00A0A011
 00A01011 00A01011
 00101011 00101011
Sentencia
Una cadena x se la denominará sentencia,
cuando la misma esté formada sólo por elementos
pertenecientes al alfabeto de símbolos terminales,
y haya sido obtenida a través de una derivación
desde el axioma de la gramática.
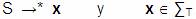
Continuando con la gramática de ejemplo
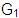 : :
Las palabras ‘1’ y
‘0011’ son sentencias de la gramática.
Forma Sentencial
Una forma sentencial x es una cadena formada
por símbolos que pertenecen tanto al alfabeto de
símbolos terminales como al de no terminales, siendo
obtenida a través de una derivación a partir del
axioma de la gramática.

En la gramática de ejemplo
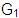 ,
las cadenas ‘00A01’, ‘00101’ y ‘000B101’ son
sentencias de la gramática. ,
las cadenas ‘00A01’, ‘00101’ y ‘000B101’ son
sentencias de la gramática.
Lenguaje
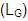
Se denomina así al lenguaje generado por una
gramática, el que estará conformado por el conjunto
de todas las sentencias o palabras que pueden ser
generados a través de la misma. En otras palabras,
serán todas las sentencias que pueden ser generadas
desde el axioma. de la gramática, con la aplicación
de todas las derivaciones que pueden aplicarse de
acuerdo al conjunto de reglas de producciones de la
gramática determinada.
Así, podemos decir que un Lenguaje posee una
Definición Formal, si existe una Gramática cuyas
producciones permitan derivar o generar sus
palabras.
El lenguaje generado por la gramática de ejemplo G1,
puede expresarse como:
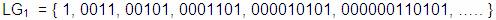
Lenguaje Formal
Así, podemos decir que un Lenguaje posee una
Definición Formal, o es un Lenguaje Formal; si
existe una Gramática cuyas producciones permitan
derivar o generar sus palabras.
Recursividad
Al analizar la recursividad en gramáticas, y por lo
tanto también en el lenguaje generado, podemos hacer
una analogía con el concepto de función recursiva en
el ámbito de la programación, donde una función es
recursiva cuando se llama a sí misma.
Producciones recursivas
Una producción es recursiva cuando el símbolo no
terminal del lado izquierdo de la regla de
producción, aparece también en el lado izquierdo de
la misma.
Las siguientes producciones son recursivas: A :=
0A1, B := BA01
Producciones recursivas por izquierda
Una producción es recursiva por izquierda cuando el
símbolo no terminal del lado izquierdo de la regla
de producción, aparece en primer lugar en el lado
derecho de la misma.
Ejemplo:
A := A1101
Producciones recursivas por derecha
Una producción es recursiva por derecha cuando el
símbolo no terminal del lado izquierdo de la regla
de producción, aparece en el último lugar en el lado
derecho de la misma.
Por ejemplo, la siguiente producción es recursiva
por derecha:
B := 0100B
Gramáticas recursivas
Una gramática es recursiva cuando posee al menos una
producción recursiva.
Recursividad en un paso
Las producciones recursivas antes mencionadas,
poseen recursividad en un paso, dado que al efectuar
una derivación, aplicando la regla de producción
recursiva, obtenemos una forma sentencial que
incluye el mismo símbolo no terminal usado al
derivar.
Recursividad en más de un paso
Otro caso de recursividad, diferente al caso
anterior, al aplicar sucesivas derivaciones,
obtenemos una forma sentencial que incluye un
símbolo no terminal, que habíamos derivado
anteriormente.
El caso más sencillo, puede verse con solamente dos
producciones:
A := B0, B := 0A100
De manera simbólica:
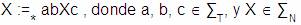
Levantamiento
de la recursividad por izquierda
La recursividad sobretodo por izquierda ya sea en un
paso o mas de un paso es un efecto no deseado en una
gramática.
El proceso de eliminación de la recursividad por
izquierda consta de los siguientes pasos:
1)
Eliminamos la recursividad por izquierda en
las producciones recursivas en un paso.
2)
Eliminamos la recursividad por izquierda en
las producciones recursivas en más de un paso.
1) Eliminación de la recursividad por izquierda
en un paso:
Eliminaremos la recursividad por izquierda en las
producciones de un
mismo símbolo no terminal.
Para cada  ,
si las producciones de A son: ,
si las producciones de A son:
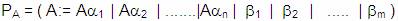
Donde los 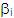 No
comienzan con A No
comienzan con A
Se crea un nuevo símbolo No Terminal A’ . En donde
ahora 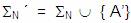
Y el nuevo conjunto de reglas de producción se
obtendrá a través del siguiente procedimiento:
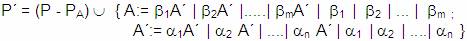
Ejemplo:
Dada la Gramática 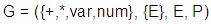
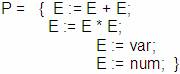
Las dos primeras reglas son recursivas por lo tanto
se creará un nuevo símbolo no Terminal E´ y el nuevo
conjunto de símbolos no terminales quedará:
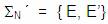
Se deberán eliminar todas las producciones de E
dentro del conjunto P de producciones de la
gramática, y se deberá obtener el nuevo conjunto P´
de producciones de la gramática. Aplicando el
procedimiento descripto.
Donde:

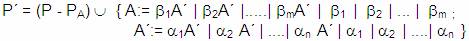

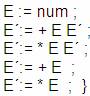
Entonces para completar la definición de la nueva
gramática equivalente a la dada, pero sin
producciones recursivas por izquierda en un paso nos
queda:

Prueba del Ejemplo:
Veremos ahora como una cadena es aceptada por ambas
gramáticas G y G´
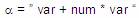
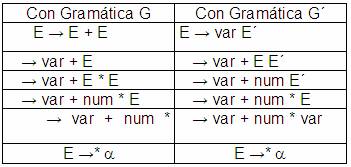
Vemos entonces que la cadena a , sería aceptada por
ambas gramáticas G y G´.
2) Eliminación de la recursividad por izquierda
en mas de un paso:
Aún eliminando, la recursividad por la izquierda de
las producciones de todos los símbolos no
terminales, puede haber recursividad en mas de un
paso.
Para mostrar el procedimiento de aplicación lo
haremos a través de un ejemplo:
Ejemplo:
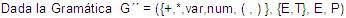
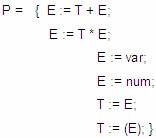
a) Se deberán disponer a los símbolos No terminales
en algún orden: 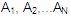
b) Se crean dos ciclos anidados que van a ir de 1
hasta n siendo n la cantidad de símbolos no
terminales de la gramática.
.i = 1 .. n
.j = 1 .. n
Recorremos ambos ciclos y :
§
Si i ¹ j :
reemplazar cada producción
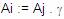 por
: por
:

Donde:
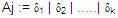 Son
todas las reglas de Aj Son
todas las reglas de Aj
§
Eliminar la recursividad por izquierda de las Ai
En nuestro ejemplo
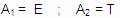
Donde n = 2 por lo tanto
.i = 1 .. 2
.j = 1 .. 2
comenzamos ambos ciclos:
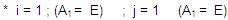
1)
En el ejemplo nos quedaría:
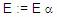
De existir producciones de E que en el lado derecho
comienza con E habría que sustituir la E de la parte
derecha por todas las producciones que llevan a E
2) Ahora hay que eliminar la posible recursión por
izquierda en
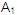 =
E pero no hay =
E pero no hay
Continuamos con el incremento de la variable del
ciclo interno.
* i = 1 ; (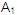 = E) ; j = 2
(
= E) ; j = 2
(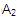 = T)
= T)
1)
En el ejemplo nos quedaría:
E := T
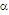
Esto da lugar a un nuevo conjunto de producciones
que se obtienen reemplazando T en la parte derecha
por todos sus producciones.
E := E + E ;
E := (E) + E ;
E := E * E ;
E := (E) * E ;
E := var ;
E := num ;
T := E ;
T := (E) ;
2)
Ahora eliminamos la recursividad por
izquierda de E. Se eliminan todas las producciones
de E y se las reemplaza por las que se obtienen de
haber incluido el nuevo símbolo no Terminal E´ (Se
aplica el procedimiento de eliminación de
recursividad en un paso).
E := var E´ ;
E := num E´ ;
E := var ;
E := num ;
E´:= + E E´ ;
E´:= * E E´ ;
E´:= + E ;
E´:= * E ;
E := (E) + E ;
E := (E) * E ;
T := E ;
T := (E) ;
E := (E) + E E´;
E := (E) * E E´;

1)
Al reemplazar las producciones:
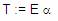
Queda:
E := var E´ ;
E := num E´ ;
E := var ;
E := num ;
E := (E) + E ;
E := (E) * E ;
E := (E) + E E´;
E := (E) * E E´;
E´:= + E E´ ;
E´:= * E E´ ;
E´:= + E ;
E´:= * E ;
T := (E) ;
T: = var E´ ;
T: = num E´ ;
T := var ;
T := num ;
T := (E) + E E´ ;
T := (E) * E E´ ;
T := (E) + E ;
T := (E) * E ;
2)
Ahora hay que eliminar las recursiones de T
pero no hay.
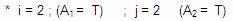
1)
Al reemplazar las producciones:
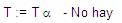
2)
No quedan:
Por lo tanto nuestra nueva gramática sin
producciones recursivas ya sean en un paso o varios
pasos nos queda:
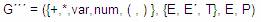
Con el conjunto de producciones de del punto
anterior.
Factorización a izquierda
Esta situación se da cuando producciones de un mismo
símbolo no Terminal, tienen en la parte derecha una
primera parte que es común a ambas producciones.
Por ejemplo:
A := cDBec ;
A := cDCb ;
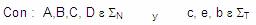
Entonces se crea un nuevo símbolo no Terminal E y
se reescriben las producciones
A := cDE ;
E := Bec ;
E := Cb ;
Árboles de derivación Sintáctica
Un árbol de derivación sintáctica es una
representación gráfica de la derivación de una forma
sentencial, desde el axioma de una gramática. Donde:
·
La raíz del árbol, representa el axioma de la
gramática.
·
Las hojas del árbol representan símbolos terminales
de la gramática.
·
Los nodos intermedios del árbol representan símbolos
no terminales de la gramática.
·
Las reglas de producción se representan como ramas
desde nodos intermedios, a nodos hijos, hojas o
intermedios; tantos como símbolos terminales o no
terminales (respectivamente) posea la regla de
producción en el lado derecho,
Ejemplo:
Dada la gramática

Donde

La cadena
 ,
puede ser obtenida a partir de la aplicación de las
sucesivas reglas de producción como sigue: ,
puede ser obtenida a partir de la aplicación de las
sucesivas reglas de producción como sigue:
A
 0B1 0B1
 00AB1 00AB1
 001B1 001B1
 001011 001011
Y el árbol de derivación sintáctico para esta cadena
quedará:

Ambigüedad
El concepto de ambigüedad en lenguajes naturales, se
aplica también en los lenguajes formales. Veremos a
continuación diversas definiciones de ambigüedad.
Una sentencia es ambigua cuando la misma puede ser
producida a través de árboles sintácticos diferentes
Ejemplo:
Dada la Gramática

Realizaremos una derivación por izquierda para
obtener la cadena a
E  E
+ E E
+ E
 id + E
id + E
 id + E * E
id + E * E
 id + id * E
id + id * E
 id + id * id
id + id * id
E
 *
id + id * id *
id + id * id
Y su grafo será:

Y si realizamos una derivación por derecha para esta
misma cadena a
E  E
* E E
* E
 E * id
E * id
 E + E * id
E + E * id
 E + id * id
E + id * id
 ( id + id) * id
( id + id) * id
E
 *
id + id * id *
id + id * id
Y el grafo correspondiente para la derivación de
esta cadena será:

Tanto con una derivación por derecha o por izquierda
se puede obtener la misma cadena pero a través de
árboles de derivación diferentes. En este caso se
dice que la cadena en cuestión es ambigua, y lo
tanto la Gramática respectiva también será ambigua.
En este caso en particular la gramática puede ser
convertida en no ambigua , o sea que se puede
levantar la ambigüedad, para esto introduciremos
reglas semánticas que establecerán el orden de
precedencia de los operadores + y *.
Para lograr esto introduciremos nuevos símbolos no
terminales:
T = Término
F = Factor
E = Expresión
Y la nueva gramática quedará:

Y sea la cadena  .
Será generada .
Será generada
E  E
+ T E
+ T
 T + T
T + T
 T + T * F
T + T * F
 F + T * F
F + T * F
 id + T * F
id + T * F
 id + F * F
id + F * F
 id + id * F
id + id * F
 id + id * id
id + id * id
E
 *
id + id * id *
id + id * id
O sea que esta nueva gramática, también es capaz de
generar la cadena, pero ahora resulta que la misma
ya no es ambigua.
Una gramática será ambigua cuando tiene al menos una
sentencia ambigua.
Tipos de Gramáticas Formales
Las gramáticas formales en base a la definición
realizada por Noam Chomsky, se clasifican en cuatro
grupos, las que van desde los tipos más general a
los tipos más específicos, dependiendo éstas de las
restricciones que se les impongan a la conformación
de las reglas de Producción (Reglas de reescritura)
De esta forma, la jerarquía propuesta nos
posibilitará: Por un lado el de poder clasificar las
gramáticas formales y por ende a los Lenguajes que
estas gramáticas generen. Y por otro lado el de
clasificar a los Autómatas que reconocerán a los
Lenguajes generados por estas gramáticas
Jerarquía de Chomsky
Toda gramática Formal, queda definida por:

En base a las restricciones que se le impongan al
conjunto P de reglas de producción, se dará origen
a los distintos tipos de Gramáticas para la
generación de lenguajes.
Además de las restricciones que se impongan para
clasificar en uno u otro tipo de gramáticas, es
común observar en las distintas bibliografías,
diferencias en su definición en lo que respecta a
que si el lenguaje generado a través de la
gramática, permitirá o no aceptar la cadena vacía.
Esto es, que si en la definición de las reglas de
producción, no se permite la definición de reglas  ,
ni siquiera desde el axioma inicial, la gramática
definida no podrá generar la cadena nula. ,
ni siquiera desde el axioma inicial, la gramática
definida no podrá generar la cadena nula.
Este punto parece no ser trivial, ya que al no
incluir reglas- no permitiría la generación de cadenas nulas. En
este material, a las gramáticas, se les permitirá la
posibilidad de generar las cadenas nulas, o sea se
les permitirá definir las reglas con
no permitiría la generación de cadenas nulas. En
este material, a las gramáticas, se les permitirá la
posibilidad de generar las cadenas nulas, o sea se
les permitirá definir las reglas con  ,
pero estarán permitidas sólo desde el axioma o
símbolo inicial de la gramática, con lo que esta
será la única regla compresora admitida por la
gramática. ,
pero estarán permitidas sólo desde el axioma o
símbolo inicial de la gramática, con lo que esta
será la única regla compresora admitida por la
gramática.

Gramáticas Tipo 3 : Gramáticas Regulares
Este tipo de gramáticas es el resultado de imponer
la mayor cantidad de restricciones a la conformación
de las reglas de producción, por lo tanto resulta
que el lenguaje que puede generar este tipo de
gramáticas es el menos expresivo (lenguaje Mínimo)
En este tipo de gramáticas las reglas de
reescrituras tendrán la siguiente forma:
Si es una G3 Lineal por Derecha
A := cB
A := a
S :=

O si es una G3 Lineal por Izquierda
A := Bc
A := a
S :=


En resumen de las reglas de producción:
Parte Izquierda
: Sólo un Símbolo No Terminal
Parte Derecha
: Podrá contener un terminal seguido de un no
terminal o un no terminal seguido de un terminal ya
sea por derecha o por izquierda, de un terminal
solamente, o producir l sólo si el no terminal de la
izquierda es el axioma inicial de la gramática
Es importante destacar que ambas gramáticas ya sean
lineales por izquierda o derecha son equivalentes
entre sí, lo que significa que generan el mismo
lenguaje, y que siempre es posible a partir de la
expresión en una determinada forma ( por derecha o
por izquierda) encontrar su equivalente.
El proceso para la conversión consta de los
siguientes pasos:
1) Se transforma la Gramática para que no haya
ninguna regla, que en la parte derecha tenga el
axioma inicial de la gramática (S)
§
Se crea un símbolo S′
§
Toda Regla S := x donde S es el axioma inicial de la
gramática y x es de la forma aB con  se
crea S′ := x se
crea S′ := x
§
Cada regla A := aS se transforma en A := a
S′
2) Se crea un grafo dirigido
§
Nodos: Existirá un nodo por cada 
§
Se crean los arcos etiquetados. En donde si A := aB
de la forma

§
Se crean arcos para cada regla  del
tipo del
tipo

§
De existir, regla de producción S :=  .
Se crea un arco sin etiqueta .
Se crea un arco sin etiqueta

3) En el grafo:
§
Se intercambian las etiquetas del axioma y de 
§
Se invierten las direcciones de los arcos
4) Se transfiere el grafo al conjunto de reglas
§
Cada Nodo
 de
la gramática excepto de
la gramática excepto

§
Cada arco etiquetado a  que
uniendo que
uniendo  con con  ,
se crea una producción de la forma A := Ba ,
se crea una producción de la forma A := Ba
§
Si existe arco del axioma a
 ,
se crea A := ,
se crea A := 
Ejemplo de conversión:
Dada la siguiente Gramática lineal por derecha,
construir la Gramática lineal por izquierda
equivalente.

P : A := 1B
A := 
B := 0A
B := 0
Aplicando el procedimiento de conversión:
Paso 1:
Se crea A′
Se crean:
A′ := 1B
A′ := 
Se transforma B := 0A en B := 0A′
Entonces ahora las reglas de producción de la
Gramática nos queda:
P : A := 1B
A :=

A′ := 1B
A′ :=

B := 0A′
B := 0
La Producción A′
:=  se
elimina ya que se
elimina ya que  sólo
puede ser producida por el axioma. sólo
puede ser producida por el axioma.
Paso 2:
Se construye el grafo dirigido

Paso 3:
Se transforma el grafo


Paso 4:
El nuevo conjunto de Reglas de Producción queda:
P : A :=

A := B0
B := 1
B := A′1
A′ := B0
En donde ahora el conjunto de reglas de producción
son LI (Lineales por Izquierda) resultan
equivalentes a las LD (Lineales por derecha)
iniciales
Gramáticas Tipo 2: Gramáticas Independientes del
Contexto
Este tipo de gramáticas también denominadas libres
de contexto o de contexto libre, son de un interés
muy particular, ya que las mismas definen las reglas
sintácticas de la mayoría de los lenguajes de
programación que son el objeto de nuestro estudio.
En este tipo de gramáticas las reglas de
reescrituras tendrán la siguiente forma:

la única regla compresora admitida es del tipo S :=  ,
siendo S el axioma de la gramática ,
siendo S el axioma de la gramática
Resumen de las reglas de producción:
Parte Izquierda
: Sólo un Símbolo No Terminal
Parte Derecha
: Sin Restricciones, excepto que sólo podrá producir  ,
si a la izquierda está el axioma inicial. ,
si a la izquierda está el axioma inicial.
Sintaxis de los
Lenguajes de programación
•
La Sintaxis en los Lenguajes de Programación es la
forma en la que se escribirán los programas.
•
Dar las reglas de sintaxis para un lenguaje
significa indicar como se escriben las
instrucciones, declaraciones y otras construcciones
del lenguaje.
•
El propósito prioritario de la Sintaxis es el de
proporcionar una notación para comunicar la
información entre el programador y el procesador de
lenguaje (Compilador).
Gramáticas Bien Formadas:
Las gramáticas, en particular las CGL
(Gramáticas de Contexto Libre), a partir de la
definición del Lenguaje que pueden generar y para
prepararlas de mejor manera para posteriores etapas
en el desarrollo de un compilador, se las debe
poder tratar eficazmente, ya sea para poder
construir el autómata con pila que sea capaz de
reconocer el Lenguaje generado por la Gramática, o
en el armado y manipulación de los árboles de
derivación sintáctico que se encuentran presentes en
todo el proceso de Compilación.
Veremos entonces, diferentes formas de
presentar a una misma gramática, que en todo momento
mantendrá la equivalencia (generarán el mismo
Lenguaje), pero serán presentadas de distinta
manera.
Una gramática está bien formada si esta
Limpia, no tiene reglas no generativas, y no tiene
reglas de redenominación.
Gramática Limpia:
Una gramática estará limpia, si no tiene
reglas innecesarias, símbolos inaccesibles, ni
símbolos superfluos (ya sean Terminales o No
Terminales)
Son las que tienen la forma:
A := A 
Este tipo de reglas de producción, ya que no
producen derivaciones útiles en la gramática.
Símbolos Inaccesibles:
Son aquellos símbolos no terminales, que nunca
podrán ser alcanzados desde el axioma inicial de la
gramática. Es decir

Ejemplo:

Observaciones:
§
La regla C := C es innecesaria, por lo tanto puede
ser eliminada.
§
Los símbolos B y C resultan inaccesibles desde el
axioma inicial, y serán eliminados en la definición
de la gramática, y también todas la reglas de
producción que los contengan. (B := 1C3 ya que C
:= C, ya fue eliminada en el paso anterior).
La gramática G2′ equivalente a G2 nos queda:

Símbolos Superfluos:
Estos pueden ser de dos tipos, Terminales, y No
Terminales
Símbolo Terminal Superfluo:
Es aquel símbolo Terminal, que nunca podrá ser
alcanzado por una derivación partiendo desde el
axioma inicial.
O sea, no existe ninguna producción

Ejemplo: En la G2′, los símbolos terminales 2 y 3
jamás podrán ser alcanzados por ninguna producción,
por lo tanto deben ser eliminados de la gramática.
Símbolo No Terminal Superfluo:
Es aquel símbolo No Terminal, del cual sus reglas de
reescritura constan del lado derecho siempre de uno
o más símbolos No Terminales. O lo que es lo mismo
que nunca producen  ,
o símbolo Terminal únicamente a través de
derivaciones. ,
o símbolo Terminal únicamente a través de
derivaciones.
Forma de proceder
para detectarlos:
1) Se marcan todos los símbolos No Terminales que
estén en la parte izquierda de una producción y en
cuya parte derecha sólo aparezcan símbolos
terminales o  . .
2) Sucesivamente, se continuarán marcando los
símbolos No terminales que estén a la izquierda de
las reglas de producción que a la derecha tengan  ,
símbolos Terminales o símbolos No Terminales
previamente marcados. ,
símbolos Terminales o símbolos No Terminales
previamente marcados.
3) Una vez finalizada estas iteraciones, se
eliminarán todos los símbolos No Terminales junto
con las producciones asociadas a ellos, de los
Símbolos No Terminales que no hayan sido marcados.
Ejemplo: Continuando con el ejercicio anterior, las
producciones de G2′

Observaciones:
§
En la primer iteración, correspondiente a T1, el
único símbolo No Terminal posible de marcar es A,
que corresponde a la Producción A :=  . .
§
En una segunda iteración, vemos que la producción D
:= 1A, a la derecha de la misma consta de un
símbolo Terminal (1) y un Símbolo No Terminal (A)
previamente marcado, por lo tanto es posible marcar
el símbolo No Terminal (D) que se encuentra a la
Izquierda.
§
Realizando una próxima iteración, vemos que no queda
ningún No Terminal a la izquierda que se pueda
marcar.
§
De esta manera resulta que el símbolo No Terminal “
E “ , resultará superfluo y se eliminará, el símbolo
y todas las producciones asociadas a éste.
Nota:
Observe que lo que se marcan
son símbolos terminales, no producciones.
Por lo tanto es posible ahora definir a G2′′ que
resultará equivalente a G2′ que a su vez es
equivalente a G2, pero que de acuerdo a su
definición no constará con reglas innecesarias,
símbolos inaccesibles, ni símbolos superfluos, ya
sean Terminales o No Terminales.

Esta gramática G2′′, será equivalente a G2, lo que
significa que ambas serán capaces de generar el
mismo lenguaje.
Una gramática limpia, para comportarse como una
gramática bien formada, no deberá contener reglas No
Generativas , ni reglas de Redenominación
Reglas No Generativas:
Una regla es No Generativa cuando produce l sin ser
el axioma de la gramática
Ejemplo:
Dada la gramática G2 = ({0}, {A,B,C},A,P)

Dentro del conjunto de reglas de producción, existen
dos reglas No Generativas, que son las que vamos a
eliminar, esas son:
B := 
C := 
Para poder eliminar una regla No Generativa, y que
la incidencia en la generación del lenguaje de la
gramática sea equivalente, es necesario que en toda
regla de producción que a la derecha aparezca el
símbolo No Terminal en cuestión proceder de la
siguiente manera. La regla tal cual esta escrita
deberá ser mantenida del conjunto de reglas de
producciones pero se deberá adicionar una nueva
regla de producción, que se obtendrá de quitarle el
símbolo No Terminar de la regla No Generativa que se
encuentre a la derecha de la regla de producción.
Comenzaremos por la primera:
B :=

Escribiremos el nuevo conjunto de reglas de
producción.

Las reglas de producciones que se encuentran
marcadas con *, son las que dan origen a las nuevas
reglas de producción que las hemos referenciado con
•, Las producciones que no hemos marcado al igual
que las referenciadas con * son mantenidas del
conjunto original de producciones.
De esta manera, ha sido posible eliminar la
producción No generativa B := l, sin perder el poder
de generación de la gramática.
Ahora partiendo de P' tomamos la siguiente regla No
Generativa
C :=


Observaciones:
El significado de los * y • con que se encuentran
marcadas las reglas de producción, tienen el mismo
significado que el descrito en P'.
Lo que ahora debe hacernos prestar atención son las
producciones que hemos identificado con *1 y *2..
En el caso de *1 ( B := B ) es una Regla
Innecesaria, por lo tanto puede ser eliminada de la
gramática, sin pérdida de generalidad en lo que
respecta a la generación de lenguaje.
En el caso de *2 (B :=  )
es una regla No Generativa que ha aparecido en el
nuevo conjunto de reglas de producciones P'', la
cual se debe eliminar aplicando nuevamente el
proceso. )
es una regla No Generativa que ha aparecido en el
nuevo conjunto de reglas de producciones P'', la
cual se debe eliminar aplicando nuevamente el
proceso.
Entonces nuevamente debemos eliminar a la regla No
Generativa
B := 
Siguiendo el mismo proceso anterior, nos queda

Esta gramática G2''' es una gramática equivalente a
G2 pero que no contiene reglas No Generativas.
Reglas de
Redenominación
Una regla es de Redenominación cuando
A := B con A,B Î
∑N
Para poder eliminarlas se borra esa regla y se
genera una nueva producción
A := x
Por cada regla B := x 
Ejemplo: Partimos de la Gramática G2'''

La regla B := C es de Redenominación y por lo tanto
debe ser eliminada.
Para eliminarla debemos proceder de la siguiente
manera:
Se eliminará la regla B := C, y se deberá reemplazar
por:
B := 0B
B := 0
Y por lo tanto la la nueva gramática nos queda:

Ejercicio 1 de aplicación:
Dada la siguiente 

Construir la gramática Bien Formada equivalente a la
dada.
Desarrollo:
Para que una gramática tipo 2 este bien formada debe
cumplir lo siguiente:
a)
Gramática Limpia
i.
Símbolos inaccesibles
ii.
Reglas innecesarias
iii.
Símbolos superfluos (Terminales y No
Terminales)
b)
Sin Reglas no generativas
c)
Sin Reglas de redenomibación
a.i ) Se buscan aquellos símbolos que no son
accesibles desde el símbolo inicial (axioma).
Los Símbolos No Terminales D y F resultan
inaccesibles, por lo tanto se eliminarán de la
gramática junto con las producciones asociadas a
éstos.
Las reglas de producción a eliminar son:
D := B1
D :=

D := 1F
F := 0D
La Gramática y el conjunto de producciones quedará:

a.ii) Reglas innecesarias NO HAY
a.iii.) Símbolos superfluos
Terminales Superfluos:
No hay ya que a la derecha de las reglas de
producción los símbolos 0 y 1 son utilizados.
No Terminales superfluos:
Efectúo procedimiento:
1) Símbolos no terminales a marcar, que en la parte
derecha tengan sólo símbolos terminales o 
Se marcan a la izquierda los símbolos No Terminales
A y B
2) Se continúa iterando pero agregando en la
evaluación a los símbolos No Terminales previamente
marcados.
Se marca ahora el Símbolo No terminal S
3) Ya no queda nada más para marcar.
Por lo tanto a la izquierda de las reglas de
producción los símbolos E y C no han podido ser
marcados por lo tanto se eliminarán de la gramática
junto con las producciones asociadas a éstos.
Las reglas que se eliminan son:
S := CS1
S := 0E
A := C
E := E1
La Gramática, ya esta limpia y nos queda:

b) Ahora buscamos las reglas No Generativas
A :=
 Esta
regla tiene que ser eliminada Esta
regla tiene que ser eliminada
Tomamos el conjunto de producciones de la gramática
y efectuamos las operaciones necesarias

Las producciones marcadas con * , son las que se
introducen al eliminar A := 
c) Eliminación de reglas de redenominación
Existen dos reglas de redenominación
S := A
S := B
Al eliminar
S := B
Introduciremos nuevas reglas de producción
S := B1
S := 1
Y al eliminar
S := A
Se introducirán:
S := 0AS
S := 0S
S := A0
S := 0
Ahora si podemos definir la Gramática CGL′′′, que
resultará equivalente a la CGL dada, pero que se
encontrará bien formada

Ejercicio 2 de aplicación:

Construir la gramática Bien Formada equivalente a la
dada.
Desarrollo:
a.i ) Se buscan aquellos símbolos que no son
accesibles desde el símbolo inicial (axioma).
NO HAY
a.ii) Reglas innecesarias
NO HAY
a.iii.) Símbolos superfluos
Terminales Superfluos:
NO HAY
No Terminales superfluos:
NO HAY
b) Ahora buscamos las reglas No Generativas
NO HAY
c) Eliminación de Reglas de Redenominación
NO HAY
Por lo tanto la gramática dada ya estaba bien
formada
Formas Normales
Las gramáticas Independientes del contexto, son las
que se utilizan de la definición de la mayoría de
los lenguajes de programación.
La definición de las Gramáticas Tipo 2 como las
hemos visto hasta ahora, cumplen con su cometido
original de cualquier punto de vista (interacción
Hombre/Máquina) se lo enfoque. Desde el punto de
vista de un usuario de un lenguaje de programación,
necesita saber exactamente cómo se debe escribir un
programa, el formato de cada proposición, su
puntuación, frases opcionales, etc. Y desde el punto
de vista del compilador (interfaz con la máquina)
necesita saber el conjunto completo de instrucciones
y programas bien escritos que debe aceptar el
traductor.
Ahora cuando nos centramos en forma estricta en el
diseño de un compilador para un lenguaje de
programación tendremos que tener en cuenta lo
siguiente:
•
Hay varias etapas y fases a cumplir y cada una de
estas tomará como entrada definiciones en etapas
anteriores.
•
El análisis sintáctico no sólo sirve para
controlar la estructura correcta de las frases
admitidas por un lenguaje de programación, sino que
prepara estructuras para usos posteriores.
•
Estas estructuras servirán para el análisis
semántico (si tiene sentido además de estar escrito
en forma correcta) y posterior generación de
instrucciones en el programa objeto.
Por tal motivo las GT2 nos deberán permitir la
utilización de algoritmos eficientes dentro de cada
una de las etapas.
Al analizar los árboles de derivación sintácticos,
éstos deben ser construidos y se entregarán como
resultado del proceso de el análisis sintáctico y el
mismo se verá afectado de acuerdo a cómo son
impuestas restricciones adicionales a la
conformación de la gramática.
La normalización de las GT2 con formas normales ya
sea la de Chomsky o la de Greibach, es sumamente
útil en el proceso de desarrollo de un Compilador,
no sólo en la fase de análisis sintáctico, sino que
tiene un alto impacto en las fases posteriores.
Las restricciones impuestas a las reglas de
producción no alteran el poder de generación de la
gramática, sino que el impacto se evidencia en cómo
se construirán los árboles de derivación
sintácticos, que se utilizarán en todas las etapas
posteriores .
Este es el producto de salida de la fase de análisis
sintáctico y es utilizado por todas las fases
posteriores.
En la etapa de síntesis sería más deseable partir de
un árbol sintáctico generado a partir de una FNC, ya
que tengo un árbol binario y por lo tanto el
algoritmo para convertir a código de tres
direcciones resulta directo.
Si tengo normalizada la gramática en FNG la ventaja
significativa la obtengo directamente en la etapa de
análisis sintáctico ya que se facilitan los
algoritmos de los Analizadores Sintácticos
LL
Partiendo de una Gramática Tipo 2 sin alterar el
poder expresivo en la definición del lenguaje que
describe, pueden obtenerse diversas formas
equivalentes dispuestas en alguna forma especial “
Normalizada “ que llamaremos formas
Normales.
Ejemplo 1
S := abcdefgS
S := abcdefg
Nos daría un Árbol sintáctico densamente tupido y
casi incontrolable en los algoritmos de recorrido
Ejemplo 2
S := A ; A := B ; B := C
C := D ; D := a ; D := A
Nos daría un árbol sintáctico inútilmente profundo y
delgado en donde los algoritmos de recorrido serian
extensos e ineficientes.
Es deseable poder establecer las restricciones
necesarias en las reglas de producción, de tal
manera que los árboles de derivación sintácticos
resultantes, no sean innecesariamente complejos o
inútilmente sencillos.
Por este motivo existen dos modelos o Formas
Normales.
Las Formas Normales de Chomsky y de
Greibach.
Para cada una de ellas vamos a determinar:
•
Restricciones impuestas a las reglas de reescritura.
•
Ventajas y desventajas de cada una.
•
Forma de obtenerlas.
•
Ejemplo práctico
Forma Normal de Chomsky (FNC)
Las reglas de producción pueden adoptar las
siguientes formas:
A := BC
A := a
S :=
 Siendo
S – Axioma Inicial Siendo
S – Axioma Inicial
Donde: 
Ventaja:
Todos los árboles de derivación son binarios y
favorecen la etapa de generación de Código
Intermedio. Siempre es posible pasar a un código de
3 direcciones BNF.
Desventaja:
Deja la posibilidad de permitir recursiones por la
izquierda en uno o más pasos, que es un efecto no
deseado en una gramática para la implementación de
algoritmos.
Procedimiento de Conversión de una GT2 en FNC
Para la conversión debe partirse por lo menos de una
Gramática limpia, es decir, sin reglas innecesarias,
sin símbolos inaccesibles y sin símbolos superfluos
Terminales y No terminales.
Para todas las producciones de la gramática, se debe
realizar:
1) Si la producción está en FNC no se hace nada y se
la deja como está
2) Si la parte derecha de la producción comienza con
un símbolo terminal.

a) Se busca si existe alguna producción en donde el
terminal en cuestión sea producido por un no
terminal. O sea si existe un C: = a y sea la única
producción de C
Si esto ocurre, a la producción original se la
remplaza por:

b) No existe ninguna producción C : = a , entonces
se crea un nuevo símbolo terminal N, que N : = a ,
y nos queda:

3) La parte derecha de la producción comienza
con un símbolo no terminal pero no continua con sólo
un No terminal

En este caso se busca si existe o se crea una
producción con un símbolo no terminal que produzca
el terminal deseado

b) 
En este caso se crea una nueva regla con un nuevo
símbolo no terminal

Si es que esta regla no existiese, quedando
A:= BN`
4) Se continúa hasta que todas las producciones
nuevas o existentes estén en FNC.
Ejemplo de Conversión de una GT2 en FNC

Desarrollo:
a) Tomo la producción 1
A : = CB2
La parte derecha comienza con un No terminal pero a
continuación hay más de un símbolo ( No terminal o
terminal ) entonces creo un nuevo símbolo no
terminal D que produce B2
D : = B2
A : = CD
La producción de A ha quedado en Forma Normal de
Chomsky, pero la nueva D no. La parte derecha de D
comienza con un no terminal pero está seguida de un
terminal.
Ahora vemos que existe una producción C : = 2
(Producción 6), y es lo único que es capaz de
producir C, o sea que la producción D sin pérdida de
generalidad como:
|
Producción Original |
Equivalente |
Forma Normal de Chomsky |
|
A := CB2 |
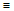 |
D := BC
A := CD |
b) Tomemos ahora la producción 2
A : = 1B
La parte derecha comienza con un símbolo terminal,
así que hay que aplicar el paso “2b”. Debe crearse
un nuevo símbolo No terminal E, ya que sólo debe
haber una regla que produzca 1
A : = EB
E : = 1
Por lo tanto nos quedaría:
|
Producción Original |
Equivalente |
Forma Normal de Chomsky |
|
A := 1B |
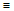 |
A := EB
E := 1 |
Las producciones 3, 4 ,5 6, ya está en FNC y no hay
que hacerles nada y la nueva G´ en FNC queda :

Forma Normal de Greibach (FNG)
Las reglas de producción pueden adoptar las
siguientes formas:

Ventaja:
Resulta una representación sumamente útil para
realizar el proceso de conversión de una GT2 a un
autómata a Pila, que se derive en un analizador
sintáctico LL.
Desventaja:
El árbol sintáctico resultante, puede no ser un
árbol binario lo que en la Generación del Código
intermedio necesitará de un proceso más laborioso.
Procedimiento de Conversión de una GT2 en FNG
1)
Si la Gramática no está limpia debe limpiarse
como primer paso.
2)
Debe eliminarse la recursividad por
izquierda.
3)
No puede haber reglas que en su parte derecha
comiencen por un símbolo No terminal.
Por lo tanto:
Se establece un orden de los símbolos No terminales,
y en las reglas que no están en FNG se producen los
reemplazos necesarios, en el orden en que han sido
fijados los símbolos No terminales.
4) Si todas las reglas están en FNG no se hace nada.
Dada la Gramática Tipo 2

1)
La gramática ya está limpia.
·
No tiene reglas innecesarias
·
No tiene símbolos inaccesibles
·
No tiene símbolos superfluos Terminales y No
terminales
2)
Eliminación de producciones recursivas por la
izquierda
La producción 3 es recursiva por la izquierda
B := BC
Para eliminarla, se aplica el teorema respectivo
para la eliminación de recursividad por izquierda,
en donde se borran todas las producciones del
símbolo B se crea un nuevo símbolo No Terminal D
quedando.
B:= BC
B:=1
En
donde tomamos
 Creamos nuevas producciones para reemplazarlas en
base al procedimiento establecido
Creamos nuevas producciones para reemplazarlas en
base al procedimiento establecido

Y nos queda
B := 1D
B := 1
D := CD
D := C
Ahora eliminamos la regla de redenominación D := C y
añadimos la regla D := 2 quedando
B := 1D
B := 1
D := CD
D := 2
El conjunto de reglas de producción hasta ahora nos
queda:

3) Se establece un orden de los símbolos No
terminales resultando - A B D C –
* Tomamos A := CB2
y generamos A:= 2B2 ya que C := 2
* Tomamos D := CD
y generamos D := 2D ya que C := 2
El conjunto de reglas de producción hasta ahora nos
queda:

4) nos queda solamente una producción que no está en
FNG
A := 2B2
Como existe una producción C := 2 y sólo existe una
sola producción C, no es necesario crear otro
símbolo adicional y la podemos reemplazar, quedando
A := 2BC
Finalmente la gramática en FNG queda:

Gramáticas Tipo 1: Gramáticas Dependientes del
Contexto
Este tipo de gramáticas también denominadas
sensibles al contexto. En este tipo de gramáticas
las reglas de reescrituras tendrán la siguiente
forma:

S := 

La única regla compresora admitida es del tipo S :=  ,
siendo S el axioma de la gramática. ,
siendo S el axioma de la gramática.
Por lo tanto, con reglas no compresoras deberá
cumplirse que:

Resumen de las reglas de producción:
Parte Izquierda
: Sin Restricciones, sólo debe contener algún
símbolo No Terminal a ser reemplazado.
Parte Derecha
: Sin Restricciones, excepto que sólo podrá producir
l, si a la izquierda está el axioma inicial.
Gramáticas Tipo 0: Gramáticas Estructuradas por
Frase
Este tipo de gramáticas, desde el punto de vista de
la informática Teórica, no despiertan mayor interés,
ya que al ser la menos restrictiva en cuanto a la
conformación de las reglas de producción, los
lenguajes generados resultan los más amplios.
También son denominadas con estructura de frase o
sin restricciones. En este tipo de gramáticas las
reglas de reescrituras tendrán la siguiente forma:

En este tipo de gramáticas son admitidas las reglas
compresoras, y esto es lo que las diferencia de las
gramáticas anteriores que sólo admitían reglas
compresoras si estas se producían a través del
axioma inicial
Resumen de las reglas de producción:
Parte Izquierda
: Sin Restricciones, sólo debe contener algún
símbolo No Terminal a ser reemplazado.
Parte Derecha
: Sin Restricciones, y admite reglas compresoras
Tablas comparativas de las Gramáticas
A continuación se presentan dos tablas, las que
permitirán identificar en forma sencilla, las
diferencias que se les han impuesto a la
conformación de las reglas de producción en lo que
respecta a clasificación de las gramáticas formales.
Clasificación de
Gramáticas
|
TIPOS DE GRAMATICAS |
Formato de las Reglas de producción |
Significado de los Símbolos |
|
Tipo 3
Regulares
Lineal por Derecha |
A := cB
A
:= a
S :=
 |

|
|
Tipo 3
Regulares
Lineal por Izquierda |
A
:=
Bc
A
:=
a
S
:=
 |
|
Tipo 2
Independientes del Contexto |
A
:=

S
:=
 |
 |
|
Tipo 2
Independientes de Contexto
Forma Normal de Chomsky |
A := BC
A := a
S :=
 |
 |
|
Tipo 2
Independientes de Contexto
Forma Normal de Greibach |
 |
 |
|
Tipo 1
Dependientes del Contexto |
 |
 |
|
Tipo 0
Estructuradas por frases |
Η
:=  |
 |
Formato de reglas de
producción
|
TIPOS DE GRAMATICAS |
Reglas de Producción |
|
Parte Izquierda |
Parte derecha |
|
Tipo 3
Regulares
|
Sólo un Símbolo No Terminal |
Podrá contener un terminal seguido de
un No terminal o No terminal seguido de
un terminal ya sea por derecha o por
izquierda, de un terminal solamente, o
producir  sólo
si el No terminal de la izquierda es el
axioma de la gramática. sólo
si el No terminal de la izquierda es el
axioma de la gramática. |
|
Tipo 2
Independientes del contexto |
Sólo un Símbolo No Terminal |
Sin restricciones, excepto que sólo
podrá producir  ,
si a la izquierda está el axioma
inicial. ,
si a la izquierda está el axioma
inicial. |
|
Tipo 1
Dependientes del Contexto |
Sin restricciones, sólo debe contener
algún símbolo No Terminal a reemplazar. |
Sin restricciones, excepto que sólo
podrá producir  ,
si a la izquierda está el axioma
inicial. ,
si a la izquierda está el axioma
inicial. |
|
Tipo 0
Estructuradas por frases |
Sin restricciones, sólo debe contener
algún símbolo No Terminal a reemplazar. |
Sin restricciones, y admite reglas
compresoras |
|

