Comenzaremos ahora a definir este tipo de máquinas que a diferencia de las máquinas secuenciales, estas poseen estado inicial previsto que es por donde comenzarán su ejecución.

 Autómatas Finitos Deterministas (AFD)

Este tipo de autómatas admite su definición de dos maneras bien diferentes:: Como autómatas traductores o reconocedores. La definición como autómatas traductores continua a la definición de las máquinas secuenciales, y se los podría definir como una subclase de estas, ya que los autómatas finitos tendrían como limitante no poder iniciar desde cualquier estado como lo hacen en las máquinas secuenciales.

La forma que adoptaremos para la definición de los autómatas finitos deterministas es como autómatas reconocedores, ya que se ajusta  con los contenidos de la informática teórica  y utilización que se les da dentro del diseño de los analizadores léxicos.

Estos autómatas solo se limitarán a aceptar o no una determinada cadena recibida en la entrada, por lo tanto podemos decir que la salida de los mismos solo tendrá dos valores posibles aceptar o no aceptar a la palabra de entrada.

Al igual que en las máquinas secuenciales, estos autómatas transitarán entre un conjunto finito de estados posibles, a medida que reciban sucesivamente los caracteres de entrada, en un instante determinado de tiempo el autómata solo podrá estar en uno y solo uno de los estados posibles.

Una característica importante de este tipo de autómatas es el determinismo, lo cuál significa que estando en un estado y recibiendo una entrada del exterior el autómata tendrá la posibilidad de transitar a uno y solo un estado del conjunto de estados posibles.

Con respecto al conjunto de estados ahora se pueden clasificar en tres tipos: Estado Inicial, que es pon donde comenzará la ejecución de la máquina; Estados finales o de aceptación que será un subconjunto del conjunto de estados por los que transitará la máquina, y si cuando se hayan terminado de procesar todos los símbolos de entrada y no reste ningún símbolo por leer, la máquina quede posicionada en uno de estos estados de aceptación, se concluirá que la cadena procesada será aceptada por el autómata. y Estados Intermedios, que tienen comportamiento idéntico a los definidos en las máquinas secuenciales.

Definición:

Los autómatas finitos deterministas quedarán formalmente definida mediante una quíntupla como sigue:

            AFD = ( ∑ , Q, q₀, F, f )

donde: 

Interpretación de funcionamiento:

Este autómata recibirá una cadena en la cinta de entrada e ira procesando de uno a la vez los símbolos de entrada. Comenzará su funcionamiento posicionada en el estado inicial, y desde este estado comenzará su ejecución.

En cada intervalo de tiempo discreto realizará dos acciones las cuales serán consideradas como acciones indivisibles en un determinado intervalo de tiempo.

Las acciones que realiza son:

·        Leer el próximo símbolo, desde la cinta de entrada.

·        Transitar, cambiar de estado 

Extensión a palabras

            El autómata finito determinista realizará transiciones de estados a través de la función f solo cuando reciba un símbolo de entrada. Esto puede generalizarse a una palabra completa, o cuando reciba la palabra vacia, en este caso se denominará una función de transición f´ como la función 

f´ :  Q x ∑*   Q

Donde:

f´ (q, ax) =  f´(f(q,a),x)

f´ (q, ) =  q                                 con a  ∑ ; x  ∑* ;  q  Q

Aceptación de Palabras:

             Una palabra será aceptada por un AFD si estando formada pos símbolos pertenecientes al alfabeto de entrada, al finalizar de procesar la misma, el autómata queda posicionado en una de los estados perteneciente al conjunto de estados finales de aceptación.

Dada:        
x    W(∑)

           f ( q_0,  x) = q_n   Si  q_n    F  la cadena x es aceptada 

Lenguaje reconocido por un AFD:

           Es el conjunto de todas las palabras reconocidas por el Autómata Finito Determinista.

            L _AFD = { x / x    ∑* y  f ( q_0,  x) = q_n con q_n    F }

Ejemplo:

             Dado el siguiente AFD definido como:

 
AFD₁ = ( ∑, Q, qi, F, f ), donde:

∑= { 0,1 } (Conjunto de símbolos de entrada del AFD)

Q= { p, q, r } (Conjunto de estados del AFD) 

qi = p  (estado inicial del AFD  (p Є Q))

F= {q } (Conjunto de estados de aceptación del AFD  ({q } с  Q))
f: función de transición de estados del AFD 

Donde la función f será:

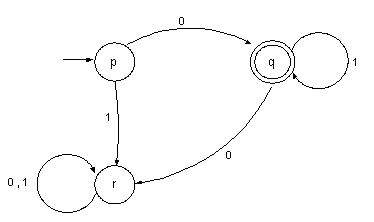
Representando su comportamiento por medio del grafo dirigido:

En donde el lenguaje aceptado por esta AFD será:

L _AFD1  = {x / x   ∑* y  x = 0.1ⁿ con n  N  0} 

Accesibilidad entre estados (A)

            Dados dos estados dentro de un autómata, se dice que uno de los  estado es accesible desde el otro, si  existe una palabra x formada por símbolos del alfabeto de entrada que hace que partiendo de este estado y a través de la aplicación de la función de transición se pueda llegar hasta  el otro.

             De esta manera definiremos:

            Sean p y q   Q dos estados dentro de un AFD y

            existe x   W(∑) tal que:

            f´( q , x ) = p  Entonces se dice que:

            pAq   ( Se lee – p es accesible desde q )

Conjunto Conexo

            Un conjunto conexo es aquel en donde todos sus estados son accesibles desde el estado inicial. Por lo tanto un  AFD será conexo si todo estado perteneciente al conjunto de estados es accesible desde el estado inicial.

Si en un AFD existieran estados que no son accesibles desde el estado inicial, los mismos pueden  ser eliminados, de manera de simplificar el autómata. Esta eliminación no afectará al comportamiento y por lo tanto continuará  aceptando el mismo Lenguaje.

Ejemplo de conjunto conexo:

            Dado el siguiente AFD definido como:

AFD₁ = ( ∑, Q, q_i, F, f ), donde:

∑= { 0,1 }

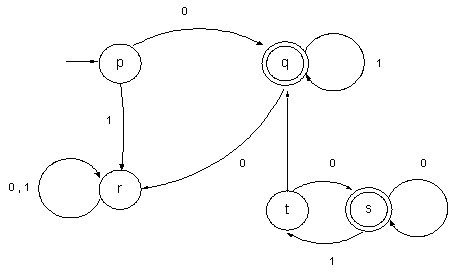
Q= { p, q, r , t, s }

q_i = p 

F= {q ,s }

Donde la función f será:

	F	0	1	También puede expresarse como:
	p	q	r	f(p, 0)= q                  f(p, 1)= r
*	q	r	q	f(q, 0)= p                  f(q, 1)= q
	R	r	r	f(r, 0)= r                    f(r, 1)= r
	T	s	q	f(t, 0)= s                    f(t, 1)= q
*	s	s	t	f(s, 0)= s                    f(s, 1)= t

El Grafo correspondiente será:

Analizando, el grafo del AFD, vemos que alos estados t y s , es imposible acceder desde el estado inicial  p, por lo tanto estos estados pueden ser eliminados del AFD y el comportamiento del autómata no se alterará.

 Equivalencias en los AFD

            A continuación presentaremos definiciones de equivalencias para culminar con equivalencia entre Autómatas Finitos Deterministas. 

Equivalencias entre estados:

Dos estados p y q serán equivalentes si: Para toda cadena  “ x ” que desde el estado p hace transitar el autómata hasta un estado de aceptación, también lo hace desde el estado q. Debiendo ocurrir simultaneamente que para toda otra cadena “ y “ que no hacen transitar desde el estado p hasta un estado de aceptación, tampoco lo hará desde el estado q.

            De esta manera definiremos:

                        Sean p y q     Q dos estados dentro de un AFD                               

                        p E q  ( Se lee:  p y q son equivalentes) 

si cadena x   W(∑) - se puede alcanzar un estado final previsto tanto comenzando desde el estado p como el de q    Y
  otra cadena y   W(∑) – no se puede alcanzar un estado final previsto tanto comenzando desde el estado p como el de q.   

  Equivalencias entre estados de longitud n:

Dos estados p y q serán equivalentes de longitud n si: cumplen la equivalencia planteada en la sección anterior pero con la restricción de que la longitud de las cadenas x e y sean menor o igual a n.

            Sean p y q   Q dos estados dentro de un AFD

            p E q  son equivalentes de longitud n si

            si      x   W(∑) , | x |  n  - se puede alcanzar un estado final previsto tanto comenzando desde el estado p como el de q  Y

           y   W(∑) ,  | y |  n – no se puede alcanzar un estado final previsto tanto comenzando desde el estado p como el de q

Equivalencia entre AFD   

             Dos AFD  A₁ y A₂  son equivalentes,
             y se dice:     A₁ E A₂

            Si ambos  autómatas aceptan las mismas cadenas o sean que reconocen exactamente el mismo lenguaje.

 Conjunto cociente Q/E

            Mediante las relaciones de equivalencias entre estados se efectúa la partición del conjunto de estados en Clases de equivalencias, en la cuál se encontrarán los estados que son equivalentes entre sí.

            Para lograr el conjunto cociente, se comienza con la relación de equivalencia entre estados de longitud 0, o sea lo que primero se intenta formar el Q/E0, y en el caso de las AFD, este conjunto se subdivide en solo dos clases, los que pertenecen al subconjunto de estados finales de aceptación y los que no pertenecen.

Q/E0 = [ {F} , {F}]

Se continuará con iteraciones sucesivas, incrementando en 1 la longitud de las cadenas de entrada en cada iteración y se verificará si los estados que siendo equivalentes en una iteración anterior continúan siendo equivalentes en la nueva clase de equivalencia Q/E1.

El proceso iterativo continuará, hasta conseguir la clase de equivalencia Q/E y este proceso se detendrá cuando un nuevo conjunto en una iteración i+1 se mantiene sin modificaciones con respecto al conjunto anterior.

 Q/E _i = Q/E _i+1  Se detiene el proceso.

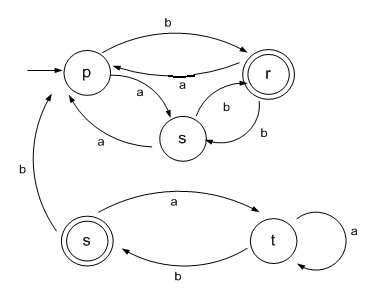
Ejemplo:

Dado el autómata, determinar el conjunto cociente mínimo

AFD₃  = ( { a , b }, { p,  q , r, s , t }, p, { r, t }, f ) , donde:

Resolución:

            Para la determinación del conjunto cociente, lo que debemos buscar son el mínimo conjuntos de estados que resultan diferentes entre sí y esto lo realizamos a través de la determinación de las clases de equivalencia entre estados.

Para ello partimos con la equivalencia de longitud 0 que corresponderá a la división en dos clases. Los estados que son de aceptación por un lado y los que no por otro lado, y luego en un proceso iterativo se continuará verificando los estados que continúen siendo equivalentes a medida que se incrementa en 1 la longitud de las estradas. El proceso finalizará cuando una clase de equivalencia se mantenga constante ante un incremento en la longitud de la entrada.

Q/E₀ = [{ F } , {F}]  =  [{ r , t }{ p , q , s }] 

Denominaremos con   c1 = {r, t} y c2 = {p,q,s}

Lo que debemos hacer ahora, es verificar si las clases de equivalencias detectadas hasta el momento ( c1 y c2) continúan siéndolo ante una nueva entrada, o sea debemos verificar si sus estados integrantes siguen siendo equivalentes al incrementar la longitud de la cadena de entrada.

c1 = {r, t}:

Al estar constituido por los estados r y t, con una nueva entrada para cada uno de esos estados deberán coincidir en que transitarán a estados que pertenecen a una misma clase de equivalencia.

Por lo tanto  f ( c1, a ) = van conjuntos cocientes diferentes de la clase anterior, y por lo tanto los estados r y t no podrán seguir siendo equivalentes. No ocurre lo mismo con una entrada b, ya que f(c1,b) van a una misma clases de equivalencia anterior.

Pero con que al menos con una entrada no vaya a una misma clase anterior, los estados r y t no serán equivalentes y por lo tanto deberán ser separados del conjunto c1.

c2 = {p, q, s}:

Veremos como transitan ante una nueva entrada (long. 1) 

Vemos que los estados p y s pertenecientes a c2 podrán continuar siendo equivalentes ya que sus salidas a las entradas respectivas caen dentro de una misma clase de equivalencia anterior. No ocurre lo mismo con el estado q que deberá ser separado de la clase de equivalencia c2.

Por lo tanto Q/E₁, nos quedará:

 Q/E1 =  [{ r } , { t } , { q }, {p , s }]

 Denominaremos con   d1 = {r} ; d2 = {t} ;  d3 = {q} ; d4 = {p,s} 

Ahora debemos comprobar, si incrementando en uno la cadena de entrada los estados p y s continúan siendo equivalentes.

d4 = {p, s}:

Veremos que pasa con una nueva entrada para cada uno de esos estados.

De esta manera, se verifica que ante una nueva entrada, los estados p y s que son equivalentes, continúan siéndolo. 

Q/E₂ =  [{ r } , { t } , { q }, {p , s }]

Vemos ahora que:  Q/E₁ = Q/E₂, por lo tanto el proceso se detiene, y las clases de equivalencias resultan: 

Q/E =  [{ r } , { t } , { q }, {p , s }]

Denominaremos con   d1 = {r} ; d2 = {t} ;  d3 = {q} ; d4 = {p,s} a los estados, y  el nuevo autómata nos quedará:

AFD₃ ´= ( { a , b }, { d1,  d2 , d3, d4 }, d4, {d1, d2}, f ) , donde:

Minimización de AFD

            El objetivo de minimización de los AFD, es obtener un autómata equivalente al dado, o sea que aceptará el mismo lenguaje,  pero este nuevo autómata  contendrá un menor número de estados.

            Los pasos a realizar para la obtención del autómata mínimo son los siguientes:

·          Se debe encontrar el autómata conexo, para estos el autómata debe cumplir que todos sus estados sean accesibles desde el estado inicial. Si existiera algún estado que no cumpliera con esta condición se lo podrá eliminar, sin que se afecte el lenguaje aceptado por el autómata.

·      Determinar el Conjunto cociente, en el cuál nos indicará el mínimo número de estados con diferente significado.

·    Construir el nuevo autómata, para ello se utilizarán los estados determinados por las clases de equivalencia. El estado inicial del nuevo autómata, pertenecerá a la clase de equivalencia en donde se encuentre el estado inicial del autómata original, y los mismo ocurrirá con los estados finales de aceptación, en donde serán los que pertenezcan a clases de equivalencias donde se encuentren estados finales de aceptación del autómata original. Con respecto a las transiciones de los nuevos estados, estas se realizarán en función a las transiciones de los estados que conforman la clase de equivalencia respectiva.     

Ejemplo: 
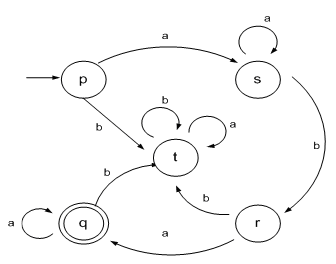
            Dado el siguiente AFD definido como:

AFD₄ = ( ∑, Q, q_i, F, f  ), donde:

∑= { a , b }

Q= { p, q, r , t, s }

q_i = p 

F= {q , r }

 Donde la función f será:

	f	a	b
	p	s	r
*	q	t	p
*	r	p	s
	s	p	r
	t	t	q

Se pide :

a)      Grafo

b)      Autómata conexo

c)      Conjunto Cociente

d)      Autómata mínimo

e)      Grafo del nuevo autómata

f)        Identificar una cadena de longitud 5 y verificar que la misma es aceptada por ambos autómatas

Resolución:

a)      Grafo del Autómata

b) Autómata Conexo

Se verifica la accesibilidad de estados desde el estado inicial, y vemos que los estados t y q resultan inaccesibles, por lo tanto pueden ser descartados y nos queda un nuevo AFD₄ ´, de la siguiente manera:

AFD₄  ´ = ( { a , b }, { p,  r , s }, p, { r }, f ´) , donde:

 Donde la función f será:

	f'	a	b
	p	s	r
*	r	p	s
	s	p	r

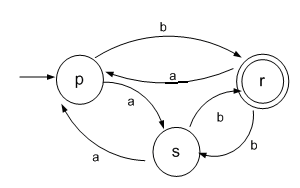
c) Conjunto cociente

Para la determinación del conjunto cociente, lo que debemos buscar son el mínimo conjuntos de estados que resultan diferentes entre sí y esto lo realizamos a través de la determinación de las clases de equivalencia entre estados.

            Para ello partimos con la equivalencia de longitud 0 que corresponderá a la división en dos clases. los estados que son de aceptación por un lado y los que no por otro lado. 

Q/E₀ = [ {p, s}, {r}]

Denominaremos con   c1 = {p, s} y c2 = {r}

Lo que debemos hacer ahora, es verificar si las clases de equivalencias detectadas hasta el momento continúan siéndolo ante una nueva entrada, o sea debemos verificar si sus estados integrantes siguen siendo equivalentes al incrementar la longitud de la cadena de entrada.

Por lo tanto, lo verificaremos para      c1 = {p, s}. Al estar constituido por los estados p y s, con una nueva entrada para cada uno de esos estados deberán coincidir en que transitarán a estados que pertenecen a una misma clase de equivalencia.

f (  p , a )  =  s

            f (  s , a )  =  p   

La salida con la entrada a son los  estados s , p que pertenecen a una misma clase de equivalencia anterior por lo tanto, podemos decir que

            f ( c1, a ) = c1 

Con respecto a la entrada b: 

f (  p , b )  =  r

            f (  s , b )  =  r 

La salida con la entrada b es el estado r por lo tanto, podemos decir que

f ( c1, b ) = c2

Con lo que se puede afirmar, que la clase de equivalencia c1, continúa siéndolo para una nueva entrada y por lo tanto:

Q/E₁ = [ {p, s}, {r}]

Ahora como Q/E₀ = Q/E₁ el proceso se detiene y   la clase equivalencia con el mínimo número de estados será

            Q/E  = [ {p, s}, {r}] =  [ {c1}, {c2}] 

d) Autómata mínimo:

AFD₄ ´´ = ( { a , b }, { c1,  c2 }, c1, { c2 }, f´´ ) , donde:

El estado inicial del nuevo autómata será c1, ya que en este se encuentra contenido el estado p que era el estado inicial del autómata equivalente.

Con respecto al estado c2, que es el estado final de aceptación, lo es ya que tiene incluido al estado r  que lo era anteriormente.  

Para el armado de la nueva función de transición, lo haremos siguiendo las transiciones originales de cada uno de los estados que componen el estado resultante de la clase de equivalencia, por lo tanto nos queda:

	f''	a	b
	c1	c1	c2
*	c2	c1	c1

e) Nuevo Grafo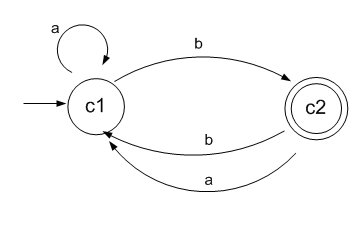

f) Verificación: 

            Dadas dos cadenas x1 y x2 ambas de longitud 5, verificaremos si ambos autómatas son capaces de reconocerlas

            x1 = aabbb

            x2 = baaab

 Para el caso del AFD₄ 

f ( p, x1 )  =  r

f ( p, x2 )  =  r

En ambas cadenas al estado que se llega es r, el cuál  pertenece al conjunto F por lo tanto ambas cadenas x1 y x2 son aceptadas por el autómata AFD_4. 

Para el caso del AFD₄´´

f ( c1, x1 )  =  c2

f ( c1, x2 )  =  c2

En ambas cadenas al estado que se llega es c2, el cuál  pertenece al conjunto F por lo tanto ambas cadenas x1 y x2 son aceptadas por el autómata AFD₄´´_.

Configuración  instantánea y  movimiento

El concepto de configuración instantánea o descripción instantánea, permite describir la configuración del autómata en cada  momento.

 Representación:  Lo representaremos mediante un par ordenado ( q, w ) en donde, q Perteneciente al conjunto de estado Q, es el estado en donde se encuentra el autómata, w formada con los símbolos del alfabeto de entrada, será la cadena que resta por leer.

Configuración Inicial:

Se establecerá como:   ( q₀ , x )  ; donde q₀  será el estado  inicial, y x la cadena a ser leida 

Configuración Final:

Se establecerá como:   ( q_n,  )  =    ; donde q_n será el estado  en donde se detiene el autómata, cuando no resta nada por leer ().

Movimiento:

Es la transición de una configuración a otra: 

( p, a )  ( q , w ) ; dados  p , q   Q ; a   ∑ ; w  ∑*

este movimiento será posible, solo si existe una transición mediante la aplicación de:

f( p , a ) = q

Implementación de un Algoritmo

            Dentro de los usos que se le pueden dar a las máquinas de estados, y en particular a los AFD, está el reconocimiento de cadenas. Para realizar este reconocimiento en forma precisa y automatizada, el mismo puede implementarse en cualquier lenguaje de programación.

Será posible que habiendo diseñado un autómata que sea capaz de reconocer un conjunto de cadenas de un lenguaje, construir un programa que implemente dicho autómata en algún lenguaje de programación, a tal fin el Algoritmo de funcionamiento del programa puede ser obtenido a partir del AFD en forma directa. 

Ejemplo:

AFD₅ = ( {0,1}, {p,q,r,s,t}, p, {q}, f  ), donde:

Donde la función f :

	f	0	1
	p	s	t
*	q	q	t
	r	q	t
	s	s	r
	t	t	t

El Grafo será:

El lenguaje aceptado por esta autómata es:

L _AFD5 =  { x / x    W(Σ)  /  aⁿ.b.a^m con n,m  1 }

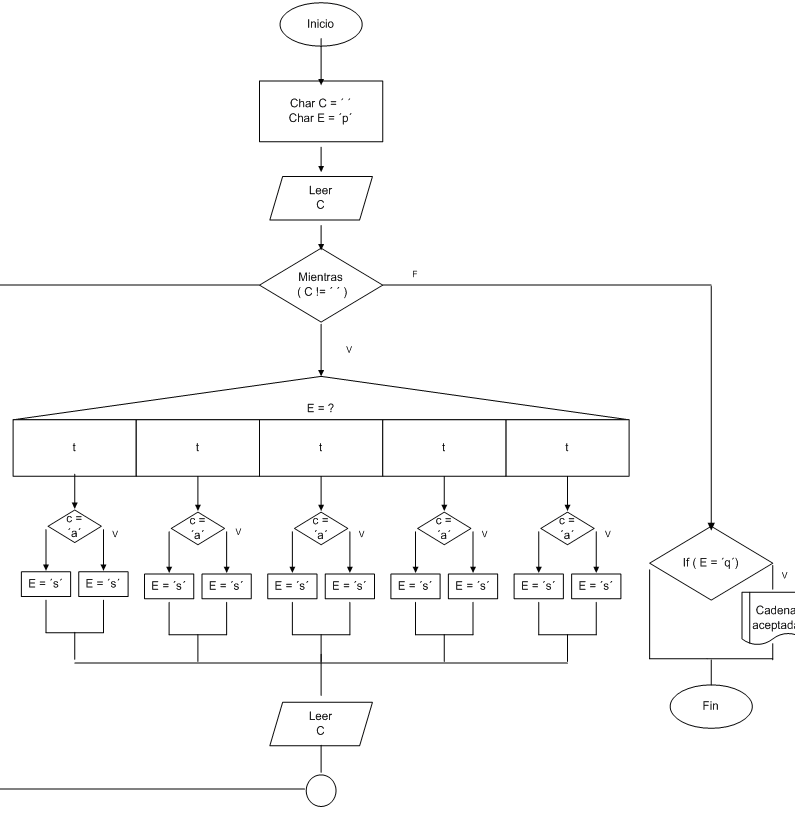
Diagrama de flujo de algoritmo:

El diagrama de flujo elemental, asumiendo que en la entrada solo se ingresarán símbolos a y b, y que siempre se ingresará al menos un carácter válido es el siguiente:

 
Hacé click sobre la imagen para verla en tamaño completo