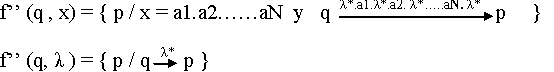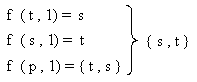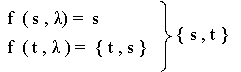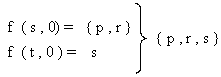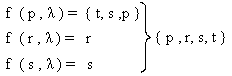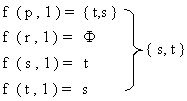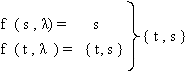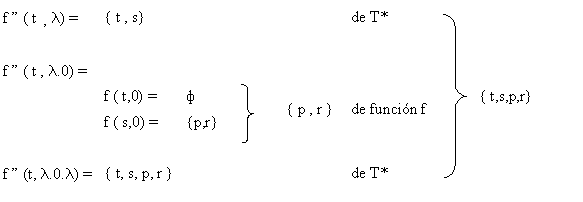Autómatas
Finitos No Deterministas (AFND)
Definición:
Un
Autómata finito determinista queda definido por un
quíntupla, al igual que en los AFD, y que su diferencia
fundamental se
encuentra, en como se definirá a la función de
transición:
AFND = (
∑ , Q, q0,
F, f )
donde:
|
∑
|
Alfabeto
de símbolos de entrada.
|
|
Q
|
Conjunto
finito de estados
|
|
q0
|
qo 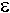 Q – estado inicial previsto Q – estado inicial previsto
|
|
F
|
F 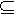 Q - es el conjunto de estado
finales de aceptación. Q - es el conjunto de estado
finales de aceptación.
|
|
f
|
Función
de transición de estados definida como
f: Q x (∑ U { 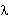 } ) → P (Q) } ) → P (Q)
En
donde P (Q), es el conjunto que se puede armar con todos los
subconjuntos de Q
|
Este
tipo de autómatas se diferencia de los AFD,
básicamente en como puede
constituirse la función de transición:. Esta
diferencias son las siguientes:
|
1)
|
Para cada par
estado entrada, el autómata puede tener la posibilidad de
transitar a mas de un
estado posible.
|
|
2)
|
Para
algún par de estado entrada, el autómata puede no
tener definido ninguna transición. Lo que significa que
podrá realizar transición alguna.
|
|
3)
|
Puede realizar
transiciones de un estado a otro sin leer símbolo alguno de
la entrada. A este tipo particular de transiciones se las denomina
transiciones-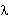 . .
|
Ejemplo:
Una
AFND puede definirse como sigue:
AFND1 = (
{ 1 , 0 },
{ p, q , r, s , t },
p,
{
r, t }, f )
, donde:
la función f puede
definirse:
En
forma
explicita:
|
f (p,0)
= r
|
f (q,1) = {s,r}
|
f (s,1)
= t
|
|
f (p,1) =
{t,s}
|
f (r,0) = p
|
f
(t, 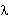 ) = s ) = s
|
|
f (p,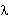 ) = t ) = t
|
f (s,0) =
{p,r}
|
f (t,1) = s
|
Tabla de doble entrada:
Al igual que en los AFD
tendremos:
· En
las filas los estados
· si
el estado es final lo
antecederá un *
· si
el estado es inicial lo marcaremos con una →
· En
las columnas se pondrán los símbolos del alfabeto
de entrada y se añadirá una
columna adicional para 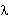
· En
la intersección (celdas de la matriz) se
indicarán las transiciones
|
|
f
|
0
|
1
|
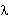
|
|
|
p
|
r
|
{t,s}
|
t
|
|
|
q
|
|
{s,r}
|
|
|
|
r
|
p
|
|
|
|
|
s
|
{p,r}
|
t
|
|
|
|
t
|
|
s
|
s
|
En la tabla f de la
función de
transición, se encuentran presentes las tres situaciones que
se admiten en los
AFND a diferencia de los AFD.
La situación
identificada como de no
determinismo propiamente dicho, en donde para un estado determinado y
ante una
misma entrada, el autómata tiene la posibilidad de transitar
a uno o mas
estado. Esta situación se presenta en tres oportunidades:
f (p,1) = {t,s}
f (q,1) = {s,r}
f (s,0) = {p,r}
y en representación
gráfica de f
(p,1) = {t,s}
sería:

La
segunda situación cuando que es no tiene definida
transición a estado alguno se
presenta en las siguientes situaciones:
f (q,0) =
f ( r,1) =
f ( t,0) =
Y la tercer
situación es cuando tiene la posibilidad de transitar de
estado, aún sin leer
ningún símbolo de la entrada, esta
situación se evidencia en las siguientes
situaciones:
f (p,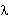 )
= t
)
= t
f (t,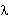 )
= s
)
= s
Gráficamente se
evidencia f (p,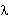 ) = q
de la siguiente
manera:
) = q
de la siguiente
manera:
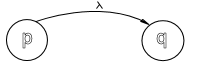
Diagrama de
transiciones:
· Cada
Nodo es un estado
· El
estado inicial tendrá un arco entrante no identificado
· Los
estados finales tendrán doble círculo.
· Existirá
un arco con sentido, etiquetado con un símbolo a entre dos
nodos p y q si
existe una transición F(p,a) = q.
Conceptos asociados a los AFND
A
continuación presentaremos un
conjunto de definiciones, que resultan necesarias, para el tratamiento
de este
tipo de Autómatas:
·
Relaciones
de Transiciones-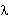 (Conjunto T).
(Conjunto T).
·
Cierre
transitivo de la relación T
; (Conjunto T*).
·
Extensión
a palabras.
·
Lenguaje
Aceptado por un AFND
·
Equivalencias
entre AFD y AFND
Relaciones de
Transiciones-λ
(Conjunto T).
Es
la relación que se establece entre los pares de estados en
que existe una
transición-λ.
Esta relación
también es reflexiva,
lo que significa también existirá una
transición λ entre los estados
contra ellos mismos, de esta manera se verifica que para todo estado
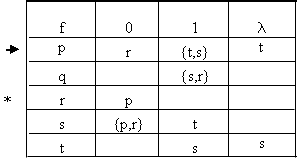
perteneciente al conjunto de estados existe f (q, λ) = q.
Con las definiciones anteriores, se
procederá a la
construcción de un
conjunto, denominado conjunto T ,
que contendrá a todos
los pares de estados, que tengan
transiciones- λ entre ellos.
En el ejemplo del AFND1 el conjunto T
resultará:
T = {(p,t)
, (t,s) , (p,p) , (q,q)
, (r,r) , (s,s) , (t,t)
}
Cierre
transitivo de la relación T
(Conjunto
T*)
Este nuevo conjunto
será calculado
aplicando la propiedad transitiva de las relación T ,
ya que se verifica que:
si
p T q y q T r entonces resulta que p T r.
En nuestro ejemplo se verifica
que
aparare un nuevo
par de estado (p,s) ya
que al aplicar la relación transitiva p T t
y t T s entonces p T
s, esta es la única regla de transitividad que se puede
aplicar, de esta manera
el nuevo conjunto T* nos quedará.
T
* = {(p,t) , (p,s) , (p,p) , (q,q)
, (r,r) , (s,s) , (t,t),
(t,s) }
Extensión a
palabras
Ahora veremos como
será el
comportamiento del AFND cuando la entrada deja de ser un
símbolo individual y
pasa a ser una cadena de caracteres, formados con símbolos
del alfabeto.
Definiremos entonces una
función f ”
:
f ¨ :
Q x ∑* →
P (Q)
en la que su comportamiento es el
siguiente:
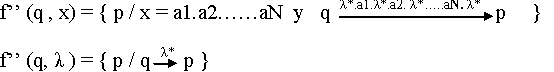
Como los AFND pueden producir
transiciones entre estados
sin leer ningún
símbolo desde el exterior, para cada uno de los estados en
donde se encuentra
el autómata hay que considerar estas
transiciones-λ.
Por lo tanto estas transiciones
se
pueden presentar antes de leer el primer símbolo, entre cada
uno de los
símbolos procesador en la entrada y también se lo
debe hacer sobre el final
cuando se ha finalizado de procesar toda la cadena de entrada.
Estas transiciones
λ* a las que
hacemos referencias son las que aparecen en el conjunto T* del cierre
transitivo de las relaciones T (transiciones-λ)
En nuestro ejemplo del AFND1 :
vamos
a calcular las transiciones que se producirán, tras recibir
en la cinta de
entrada la cadena 101, entonces:
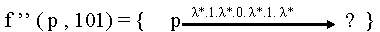
Lo
primero que debemos realizar previo a
la entrada del primer símbolo, es aplicar si existieren las
relaciones de
transiciones-λ, y entonces como primer paso se debe aplicar:
f ‘’ ( p ,
λ) =
Y entonces lo que
hacemos es buscar
si existen relación de
transiciones dentro
del conjunto T* = {(p,t) , (p,s) , (p,p) , (q,q)
, (r,r) , (s,s) , (t,t),
(t,s) }
y lo que se obtiene
es lo siguiente:
f ‘’ ( p ,
λ) = {t,s,p}
Entonces
significa, que el autómata podrá estar en
cualquiera de los estados t ,
s , p antes de recibir la primer entrada, por lo tanto
se deberá ver cual serán las transiciones
(aplicación de la función de
transición f) con la entrada para cada uno de los estados
respectivos.
Ahora
entonces aplicamos la función f
, para el primer
símbolo de la entrada.
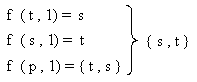
Entonces
lo hecho hasta ahora es :
f ‘’ ( p , λ.1 ) = { s , t }
Ahora
nuevamente debemos aplicar el conjunto T* para determinar, si desde los
estados s ,
t es posible que el
autómata transite
sin leer nada de la entrada. Al aplicar nuevamente el conjunto T* y nos
quedará:
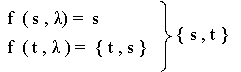
Hasta el momento tendremos
: f ‘’ ( p , λ.1.λ ) = { s , t }
Veremos ahora a que estados
podrá
transitar ante la lectura de la próxima entrada:
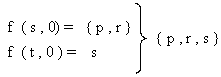
Y hasta el momento tendremos
: f ‘’ ( p
, λ.1.λ.0 ) = { p, r, s }
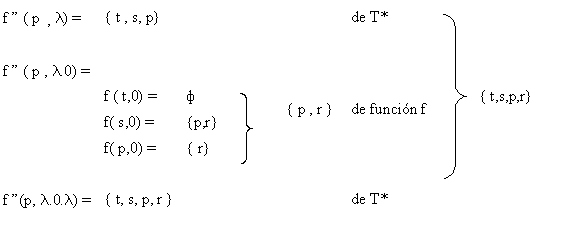
Nuevamente aplicaremos el
conjunto
T* y tenemos:
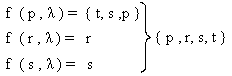
Y hasta el momento tendremos
: f ‘’ ( p
, λ.1.λ.0.λ ) = { p, r, s, t }
Nuevamente tomaremos al
próximo
símbolo de entrada “1”
que será el último que tenemos que procesar, y
por lo tanto aplicamos la
función f.
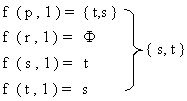
Vemos que f
( r , 1 ) =
Ф, no
tiene definida transición alguna, por lo
tanto la descartaremos y nos quedará.
Y hasta el momento tendremos
: f ‘’ ( p
, λ.1.λ.0.λ.1 ) = { s, t
}
Ahora nos falta aplicar sobre
el
final de la cadena de entrada, si existe transición
λ sobre los
estados ( s, t
) , para ello aplicamos por última vez T*
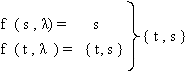
Y finalmente tendremos
: f
‘’ ( p , λ.1.λ.0.λ.1.λ ) = { s,
t };
Esto significa que partiendo
del
estado inicial p y recibiendo la cadena de entrada 101,
y al
seguir todos las combinaciones posibles de transiciones de estados
(todos los
caminos que se pueden presentar), el autómata solo
podrá quedar posicionado en
el conjunto de estados {s ,
t} que esta formado
por los estados
s o t ,y
como el estado t pertenece al conjunto de estado
finales de aceptación,
se dice que la cadena es aceptada por el AFND
Lenguaje
Aceptado por un AFND
Será
el conjunto de palabras que le hacen transitar desde el estado inicial
a algún
estado de finalización utilizando la función f
’’.
L AFND =
{ x / x
ε ∑*
y f “(q0 , x) ∩ F ≠ ∅
}
Significa
que el lenguaje aceptado por un AFND estará constituido por
todas las cadenas
formadas con símbolos del alfabeto de entrada, que partiendo
desde el estado
inicial, el autómata quedará posicionado en un estados
que pertenezca al conjunto de estados finales de aceptación.
Equivalencias
entre AF Determinista
y No determinista
La
equivalencia entre autómatas AFD y AFND, siempre es posible,
y esto significa
que siempre se podrá dado uno de ellos obtener su
equivalente. Por lo tanto, se
podrá asegurar que ambos, AFD y AFND reconocerán
el mismo lenguaje.
Conversión
de AFD a AFND :
Es fácil ver que los
AFD son una
particularización de los AFND, ya que: por un lado no
existirán transiciones-λ y por otro lado, las transiciones siempre
producirán un estado determinado. Así tendremos
que:
-
No existirán
transiciones-λ por lo tanto:
f” (q, λ) = ф.
-
| f (p,a)|
= 1 ; Siempre se
transita a un solo estado
Conversión de AFND a AFD:
Vamos a construir un AFD
partiendo
de un AFND, donde:
AFND = (
∑ , Q, q0, F, f
)
AFD
= ( ∑ , Q´,
q0´, F ´, f ´
)
donde para la conversión
se tendrá en
cuenta:
·
Q´ = P(Q)
·
q0´
= f” (q0, λ)
; El
nuevo estado inicial, se obtiene en forma directa de T*.
·
F´ = {
c / c ε
Q´ Si existe q ε c y
q ε
F } Un
estado perteneciente al nuevo conjunto de estados será de
finalización o
aceptación, solo si esta constituido por estados que eran de
aceptación en el
autómata en el AFND de origen.
·
f´(c,a)
= { c / c ε
Q´
=
∪ q 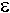 c f
” (q,a)
c f
” (q,a)
Lo que se
hará primero es calcular
q0´ y luego se irán
calculando los demás estados Q´
obtenidos a partir de P(Q)
a
medida que van presentando en el proceso de conversión.
Ejemplo:
Dado:
AFND1 = (
{ 0 , 1 },
{ p, q , r, s , t },
p,
{
r }, f )
, donde:
Obtendremos
ahora el AFD equivalente.
T = {(p,t)
, (t,s) , (p,p) , (q,q)
, (r,r) , (s,s) , (t,t)
}
T*
= {(p,t) , (p,s)
, (p,p) , (q,q) , (r,r)
, (s,s) , (t,t), (t,s)
}
Nuevo
estado inicial c0
= f “ ( p, 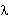 )
; lo obtendremos de T*
)
; lo obtendremos de T*
Para el
estado t 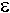 c0 :
c0 :
Para el
estado s ε c0 :
Para el
estado t ε c0 :
De esta manera
:
f´( c0 ,
0 ) = {
∪
(ⓐ,
ⓑ, ⓒ)
}
Por lo
tanto: f
´ (c0 ,
0 ) = { t, s, p, r } =
c1
De igual
manera calcularemos a c0 pero ahora con entrada
1, pero
simplificando la representación de los pasos y nos queda:
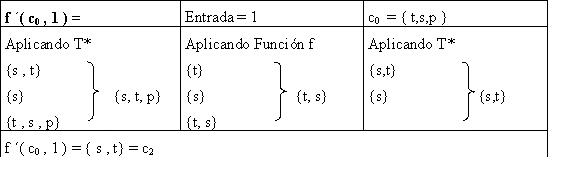
Ahora
debemos para cada uno de los estados que vaya apareciendo, como se va
comportando
ante ambas entradas. Tomamos ahora el estado c1 = {
t,s,p,r
}
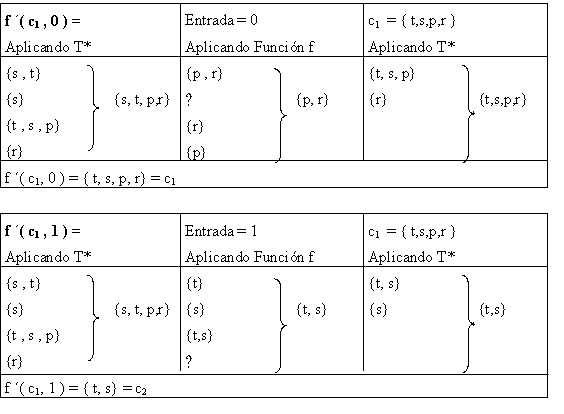
Ahora
tomamos c2 = { t, s}, y
vemos como se comportará la función de
transición f ´ ante nuevas entradas 0 y
1, respectivamente.


Vemos
ahora que no se ha creado ningún nuevo estado, por lo tanto
hemos terminado el
proceso de construcción de la función f
´ y de el conjunto Q ´.
|
Nuevo estado 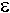 Q ´
Q ´
|
P(Q)
|
|
c0
|
{ t,s,p
}
|
|
c1
|
{ t, s, p, r}
|
|
c2
|
{ s , t }
|
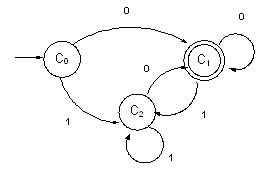
Ahora
estamos en condición de formalizar el AFD equivalente al AFND1
AFD = (
{ 0 , 1 },
{ c0 ,
c1, c2
},
c0 , { c1
}, f ´) , donde:
Los estados finales de aceptación en el
ADND,
es el conjunto F = { r
}, por lo tanto F ´
estará conformada por todos los nuevos estados que incluyan a dicho estado. Entonces el estado c1
será
estado de aceptación del nuevo autómata.
Donde la función de transición será:
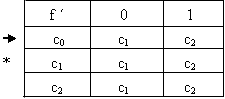
Y el grafo del AFD quedará :