|
Estas
máquinas, son en esencia máquinas traductoras, ya
que dada una palabra en la entrada generan otra palabra en la salida.
Por lo expuesto en el párrafo anterior, para poder
producir la correspondiente transformación estas
máquinas deberán estar compuestas por:
• Dos cintas asociadas, una que
permita alojar una cadena de símbolos a la entrada, que
serán leídos uno por vez, y otra cinta
que permita registrar las salidas que se irán produciendo en
la ejecución de la máquina.
• Deberán contener un
conjunto finito de estados, los que son capaces de memorizar, en cada
momento la parte de la palabra de entrada leída en ese
instante de tiempo, cambiar de estado y producir una salida.
Es importante resaltar que en un determinado intervalo de tiempo, las
máquinas secuenciales realizarán tres
acciones que serán indivisibles (consideradas como una
unidad), las cuales son:
-
Realizan una lectura sobre la cinta de entrada.
-
Cambiar de estado.
-
Grabar un símbolo en la cinta de salida
Otro característica importante a destacar sobre este tipo de
máquinas, es que no disponen de un estado inicial previsto,
por lo tanto en el momento de comenzar su funcionamiento
podrán hacerlo desde cualquiera de sus estados, produciendo
eventualmente salidas diferentes.
2.5.1.
Máquina de Mealy (ME)
Esta
máquina la simbolizaremos con ME, y quedará
formalmente definida mediante una quíntupla como sigue:
ME
= {
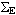 , ,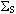 , Q, f, g} , Q, f, g}
|
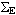 |
Conjunto
de símbolos de entrada |
|
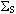 |
Conjunto
de símbolos de salida |
|
Q |
Conjunto
finito de estados |
|
f |
Función
de transición de estados definida como
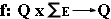
|
|
g |
Función
de salida definida como
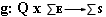 |
Interpretación
La
máquina de Mealy permanece en un cierto estado mientras no
recibe ningún estímulo del exterior. Cuando
recibe un símbolo del exterior (Perteneciente al conjunto de
símbolos de entrada) realiza otras dos acciones en forma
simultánea:
1-
Transita a otro estado (que puede ser el mismo en el que
está pero igual se produce el transito) . De acuerdo con la
función de transición f
2-
Emite un símbolo a la salida (símbolo que
pertenece al conjunto de símbolos de salida). de acuerdo con
la función de salida
Estas tres acciones:
lectura de un símbolo desde exterior (cinta de Entrada),
Transición de estado, y Grabado (Cinta de Salida),
serán indivisibles dentro de un intervalo de
tiempo.
De esta
manera al transitar desde un intervalo de tiempo discreto i
hasta i+1 la máquina realizará:
|
Acción |
Significado |
|
q
i+1 = f( qi, ei) |
Estando
en el intervalo de tiempo i en el estado
qi y recibiendo
desde la cinta de entrada
ei, la máquina transita al estado qi+1
|
|
Si
= f( qi, ei) |
Que la salida producida en el
intervalo de tiempo i estará solo en función del
estado en que se encuentra en ese tiempo i, y la salida que
producirá será la correspondiente al
símbolo del estado que este después de realizar
la transición.
|
Si analizamos esta máquina en
relación a la máquina
de Mealy, notamos que la diferencia que existe entre ambas radica solo
en como
se comporta la función de salida q
Ejemplo:
Describiremos una máquina de Moore, que resuelve el mismo
ejercicio resuelto por la Máquina de Mealy anterior.
La
máquina nos queda:
MO
= ({0,1}, {p,i}, {q0,q1},
f, g)
Descripción
explícita de la funciones f y g

Tablas de doble entrada:
Función
Transición f

Grafo:
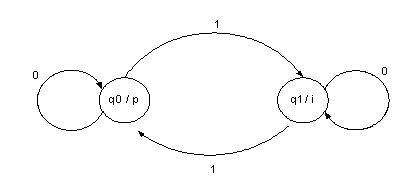
Resultado de ejecución
De igual manera que en el ejemplo de
Mealy probaremos el funcionamiento
de la máquina de Moore sobre las mismas cadenas:
a) Que salida le corresponderá
a una entrada 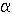 1 = 0100 , comenzando
la ejecución
de la máquina por el estado q0. 1 = 0100 , comenzando
la ejecución
de la máquina por el estado q0.
La salida producida para la entrada 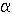 1, será
: piii 1, será
: piii
b) Que salida le corresponderá
a una entrada 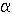 2 = 1011100 ,
comenzando la
ejecución de la máquina por el estado q0. 2 = 1011100 ,
comenzando la
ejecución de la máquina por el estado q0.
La salida producida para la entrada 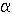 2,
será
: iipippp 2,
será
: iipippp
2.5.3. Comparación de
representación entre Máquinas Mealy y Moore
Con respecto a la ejecución de
ambas máquinas de acuerdo a los ejemplos anteriormente
resueltos, notamos que para las mismas cadenas de entrada, y comenzando
por el mismo estado, se obtendrán las mismas salidas.
Las diferencias que se observan, con respecto a las diferentes formas
de representación entre las máquinas
radican fundamentalmente en las diferencias que tienen ambas
máquinas en la constitución de la
función de salida g.
Ahora si analizamos las diferentes formas de representación
de las funciones f y g notamos lo siguiente:
Con
respecto a la notación explícita, vemos que lo
que cambia es la definición de la función
g ya que en Moore la salida dependerá solamente
del estado al que transitará la máquina.
Con respecto a las tablas, notamos que en Moore en el caso de la
representación de la función g, dejará
de ser una matriz como es en el caso de Mealy para convertirse en
un vector.
Con respecto al grafo, los cambios que se producirán son en
la rotulación de las transiciones, ya que en Moore solamente
se deberá indicar que entrada produce la
transición de estado, y en la rotulación del
estado ahora se deberá indicar también
cuál es la salida que producirá.
2.5.4. Equivalencia entre
Máquinas de Mealy y Máquina de Moore
Las funciones de salidas de ambas
máquinas se representan como sigue:
|
MEALY |
g
: Q x 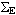 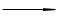 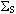
|
|
MOORE |
g
: Q 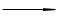 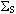
|
Por lo tanto las salidas correspondientes
en un determinado tiempo i se obtendrán de la siguiente
manera:
|
MEALY |
Si
= f( qi, ei)
|
Que
la salida producida en el intervalo de tiempo i estará en
función
del estado en que se encuentra y la entrada que recibe en el mismo
tiempo i |
|
MOORE |
Si
= f( qi ) |
Que
la salida producida en el intervalo de tiempo i
estará solo en función del estado en que se
encuentra en ese tiempo i,
y la salida que se producirá será la
correspondiente al símbolo del
estado que este después de realizar la transición |
Básicamente la diferencia
entre ambas máquinas está dada en la respuesta
que producen ambas máquinas secuenciales.
En la máquina de Mealy se dice que la respuesta es inmediata
ya que la salida la produce en forma directa después de
recibir la entrada. Mientras que en la máquina de Moore, la
respuesta solo depende del estado en que se
encontrará la máquina después de
realizar cada transición.
De acuerdo a lo expresado anteriormente, se puede demostrar
que la salida en una máquina de Moore, experimenta un
retardo de tiempo respecto de su entrada. Esta apreciación
es razonable, ya que la respuesta depende solo del estado al que
transitará la máquina pero esta
transición se deberá a la entrada anterior que
dio origen al estado en el cuál se encuentra la
máquina.
En Moore: En un determinado intervalo de tiempo i la máquina
se encuentra en un determinado estado qi, y recibe un
símbolo ei y se producirá una
transición de estado y una salida como sigue:
f ( qi , ei ) = q
i+1
g ( qi ) = si
pero para haber estado en el estado qi que produjo la
salida si debió
en un intervalo de tiempo anterior haber recibido una entrada que lo
llevo a este estado.
f ( qi-1 , ei-1 ) = q i
g ( qi ) = g (f ( qi-1
, ei-1 )) = si
En donde se evidencia que la salida si
en la máquina de Moore en un intervalo i depende en forma
directa de la entrada ei-1
2.5.5. Conversión de
Máquinas Secuenciales
Toda máquina de Mealy se puede
transformar en
una máquina de Moore y viceversa. Los
procedimientos
serán los que siguen.
2.5.5.1. De
Mealy a Moore:
Dada la Máquina de Mealy:
ME = {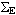 , , 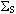 , Q, f, g}
Construiremos La Máquina de Moore , Q, f, g}
Construiremos La Máquina de Moore
M0 = {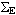 , , 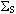 , Q´, f´,
g´} de la siguiente manera. , Q´, f´,
g´} de la siguiente manera.
En donde por cada combinación
de estado/entrada :
f ( q , a ) = p
g ( q , a ) =
b
( con q,p 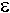 Q ; a
Q ; a 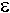 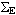 ; b
; b 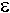 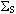 ) )
Se crea:
1)
Un
estado: pb
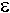 Q´
, al que le corresponderá la siguiente
función salida: Q´
, al que le corresponderá la siguiente
función salida:
2)
Una transición: f´( qs
, a ) = pb
, para
cada estado qs , s 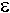 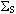
Si a un determinado estado q 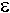 Q no
llegase ninguna transición, se creará un nodo
etiquetado con q Q no
llegase ninguna transición, se creará un nodo
etiquetado con q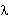 . .
Ejemplo:
Dada la máquina de
Mealy
ME1
= ({0 , 1}, {a
, b}, { r, s, t }, f, g)
|
|
Función
Transición f
|
|
|
Función Salida
g
|
|
|
|
|
|
|
|
|
|
|
|
|
f
|
0
|
1
|
|
|
g
|
0
|
1
|
|
|
r
|
r
|
t
|
|
|
r
|
a
|
b
|
|
|
s
|
r
|
s
|
|
|
s
|
a
|
b
|
|
|
t
|
r
|
s
|
|
|
t
|
b
|
a
|
Su grafo:
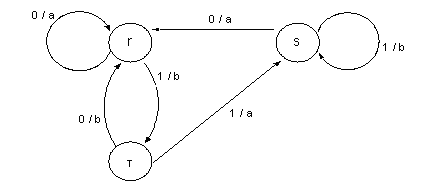
y la salida que corresponde a una
entrada 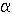 = 00011001 comenzando en el estado
r
será :
aaabaaab = 00011001 comenzando en el estado
r
será :
aaabaaab

Ahora comenzaremos el proceso
de
conversión a una máquina de Moore equivalente:
MO1
= ({0 , 1}, {a , b}, Q´, f´, g´)
donde:
f(r, 0) = r
,
g(r, 0) = a
Entonces:
ra 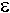 Q’ ;
g´( ra)
=
a ; f´( ra
, 0 ) =
ra
; f´(
rb , 0 )
= ra Q’ ;
g´( ra)
=
a ; f´( ra
, 0 ) =
ra
; f´(
rb , 0 )
= ra
f(r, 1) = t
,
g(r, 1) = b
Entonces:
tb 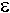 Q’ ;
g´( tb)
=
b ; f´( ra
, 1 ) =
tb ;
f´( rb , 1 )
= tb Q’ ;
g´( tb)
=
b ; f´( ra
, 1 ) =
tb ;
f´( rb , 1 )
= tb
f(s, 0) = r
,
g(s, 0) = a
Entonces :
ra 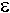 Q’ ;
g´( ra)
=
a ; f´( sa
, 0 ) =
ra ;
f´( sb , 0 )
= ra Q’ ;
g´( ra)
=
a ; f´( sa
, 0 ) =
ra ;
f´( sb , 0 )
= ra
f(s, 1) = s
,
g(s, 1) = b
Entonces:
sb 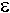 Q’ ;
g´( sb)
=
b ; f´( sa
, 1 ) =
sb ;
f´( sb , 1 )
= sb Q’ ;
g´( sb)
=
b ; f´( sa
, 1 ) =
sb ;
f´( sb , 1 )
= sb
f(t, 0) = r
,
g(t, 0) = b
Entonces:
rb  Q’ ;
g´( rb ) = b
; f´(
ta , 0 )
= rb
; f´( tb
, 0 ) =
rb Q’ ;
g´( rb ) = b
; f´(
ta , 0 )
= rb
; f´( tb
, 0 ) =
rb
f(t, 1) = s
,
g(t, 1) = a
Entonces:
sa  Q’ ;
g´( sa)
= a
; f´(
ta , 1 )
= sa
; f´( tb
, 1 ) =
sa Q’ ;
g´( sa)
= a
; f´(
ta , 1 )
= sa
; f´( tb
, 1 ) =
sa
Nos quedará entonces: Q´ =
{
ra
, tb , sb , rb ,
sa },vemos
entonces que el estado ta
,nunca ha sido creado, por lo
tanto se anularán todas las transiciones
correspondientes a dicho estado.
|
Función Transición f´
|
|
Función Salida
g’
|
|
|
|
|
|
|
|
|
|
f ´
|
0
|
1
|
|
|
g´
|
|
|
ra
|
ra
|
tb
|
|
|
ra
|
a
|
|
tb
|
rb
|
sa
|
|
|
tb
|
b
|
|
sb
|
ra
|
sb
|
|
|
sb
|
b
|
|
rb
|
ra
|
tb
|
|
|
rb
|
b
|
|
sa
|
ra
|
sb
|
|
|
sa
|
a
|
Y el grafo correspondiente a la
máquina quedará:

Si ahora, analizamos el
comportamiento de esta máquina de moore, para la misma
cadena aceptada por la
máquina de mealy equivalente vemos lo siguiente. Para
determinar por cual
estado debemos comenzar lo haremos por aquellos estados que
participaron en el
misto estado r de la máquina de mealy, estos
estados serán (ra
y rb
)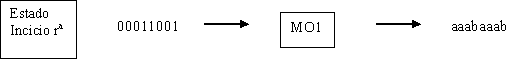
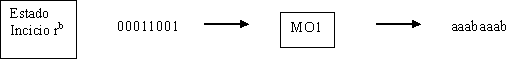
Donde se evidencia que la
máquina de
Moore responde de igual manera que la Máquina
de Mealy
2.5.5.1.
De
Moore a
Mealy :
Dada la Máquina de
Moore:
MO = {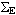 , , 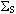 , Q, f, g} Construiremos La Máquina
de Mealy , Q, f, g} Construiremos La Máquina
de Mealy
ME = {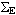 , , 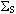 , Q, f, g´}
de la
siguiente manera. , Q, f, g´}
de la
siguiente manera.
En donde por cada transición y
salida en el que se cumpla :
f ( q , a
) = p
g ( q ) =
b
( con q, p
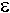 Q ; a Q ; a 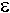 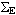 ; b ; b 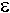 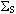 ) )
Se define:
g´(
q , a ) = b
Ejemplo:
Dada la máquina de
Moore
MO2
= ({0 , 1}, {a
, b}, { r, s }, f,
g)
|
|
Función Transición f
|
|
Función Salida
g
|
|
|
|
|
|
|
|
|
|
|
|
f
|
0
|
1
|
|
|
g
|
|
|
|
r
|
r
|
s
|
|
|
r
|
a
|
Grafo:
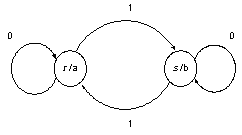
y la salida que corresponde a una
entrada 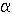 = 00100111 comenzando en el estado
r será : aaabaaab = 00100111 comenzando en el estado
r será : aaabaaab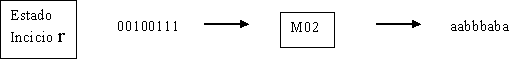
Ahora
comenzaremos el proceso de
conversión para obtener a una máquina de Mealy
equivalente:
ME2
= ({0 , 1}, {a , b}, Q, f, g´)
donde:
f ( r , 0 ) =
r
; g
( r ) = a ;
Por lo tanto
g’ ( r , 0 ) = a
;
f ( r , 1 ) =
s
; g
( s ) = b ;
Por lo tanto
g’ ( r , 1 ) = b
;
f ( s , 0 ) =
s
; g
( s ) = b ;
Por lo tanto
g’ ( r , 0 ) = b
;
f ( s , 1 ) =
r
; g
( r ) = a ;
Por lo tanto
g’ ( r , 1 ) = a
;
por lo tanto las funciones f y
g´
quedarán:
|
Función Transición f
|
|
|
Función Salida
g´
|
|
|
|
|
|
|
|
|
|
|
|
f
|
0
|
1
|
|
|
g´
|
0
|
1
|
|
r
|
r
|
s
|
|
|
r
|
a
|
b
|
|
s
|
s
|
r
|
|
|
s
|
b
|
a
|
y la salida que corresponde a
una
entrada
a = 00100111 comenzando en el
estado
r será : aaabaaab
igual
que en la máquina de Moore equivalente. |

